①等温过程：T＝常数

②等压过程：p＝常数

③等容过程：ρ＝常数

④等熵过程：（可逆绝热过程）

将上述过程方程代入运动方程，可分别得到各自的能量方程。

对于等温过程，即

对于等熵过程，即(www.daowen.com)

式（11．24）和前面的式（11．16）、式（11．17）完全相同，称为等熵气流的能量方程。

实际中，常用多变指数n代替绝热指数k，此时有：

式中，等温n＝1；绝热n＝k，等容n＝±∞。

对于等熵流动的式（11．16）、式（11．17）或式（11．24），与不可压缩流体能量方程比较，由于绝热变化使压能增大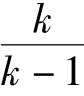倍，对于空气有：。

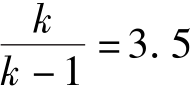需要指出的是，能量方程式（11．17）不仅对一元恒定理想绝热（等熵）气流适用，而且对一元恒定有摩擦绝热气流也是适用的。因为在管壁为绝热的有摩擦气流中，流体克服摩擦力做的功等于加给流体的摩擦热，两者在能量方程式（11．11）中互相抵消，并不影响能量的平衡，能量方程的形式也不改变，不过气体的熵值增大，因而可用（有效）能量减小。等熵流动与摩擦绝热流动的不同在于：如两者在第一断面的参数相同，在第二断面上的某些参数却不同。

由上面分析可知，连续性方程、能量方程、状态方程和过程方程构成了一元恒定气流的基本方程，利用基本方程就可以求出两个有效断面之间的u、p、ρ、T四个参数的关系。