【摘要】:此时,热力学第一定律表示为:加给控制面中单位质量流体的热量,用来增加其内能、动能和克服外力做功,即图11.4推导能量方程图式中,dq为加给控制面中单位质量流体的热量;de和d是单位质量流体的内能和动能的增加;dl为单位质量流体克服所有外力做的功。
在一元恒定气流中取如图11.4所示的控制面,且设流体为理想流体。此时,热力学第一定律表示为:加给控制面中单位质量流体的热量,用来增加其内能、动能和克服外力做功,即

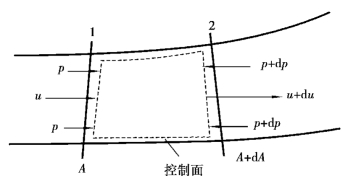
图11.4 推导能量方程图
式中,dq为加给控制面中单位质量流体的热量;de和d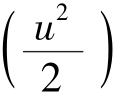 是单位质量流体的内能和动能的增加;dl为单位质量流体克服所有外力做的功。规定流体克服外力做的功为正。dl包括克服质量力、总压力做的功dlg、dlp,以及外界加入的机械功dle,即dl=dlg+dlp-dle。对气体,可忽略质量力的影响,于是,dlg=0。下面讨论克服总压力做的功:
是单位质量流体的内能和动能的增加;dl为单位质量流体克服所有外力做的功。规定流体克服外力做的功为正。dl包括克服质量力、总压力做的功dlg、dlp,以及外界加入的机械功dle,即dl=dlg+dlp-dle。对气体,可忽略质量力的影响,于是,dlg=0。下面讨论克服总压力做的功:
设控制面进入断面1上的压强、速度、面积为p、u、A,控制面流出断面2上的压强、速度、面积为(p+dp)、(u+du)、(A+dA),控制面侧表面为流面。克服作用在控制面上总压力做的功为
dLp=[(p+dp)(A+dA)(u+du)-pAu]dt
展开上式并忽略高阶无穷小量后得
dLp=[pAdu+pudA+uAdp]dt=[pd(uA)+uAdp]dt
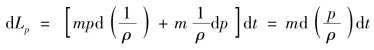
对控制面中单位质量流体来说,克服总压力做的功为
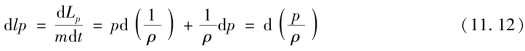 (www.daowen.com)
(www.daowen.com)
式中 pd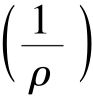 ——流体单位质量的体积压缩功或体积膨胀功;
——流体单位质量的体积压缩功或体积膨胀功;
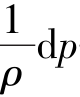 ——流体单位质量的移动功。
——流体单位质量的移动功。
于是式(11.11)可写为
![]()
引用热力学中焓的概念,即对于完全气体有di=de+d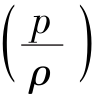 ,于是,上式可写为
,于是,上式可写为
![]()
再如流动为绝热且无外加机械功,则得一元恒定等熵气流的能量方程的微分形式为
![]()
积分得

由热力学知,对于完全气体有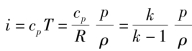 ,故上式可写为
,故上式可写为
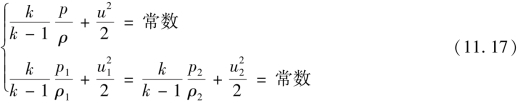
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
有关工程流体力学的文章

 ,这里m为质量
,这里m为质量



