从大量的实际观察和理论分析知道，决定流场流型的主要因素有：扰动物体的形状、介质的属性以及流速与流场上原存在的音速（即远方未经扰动气流的音速）之比。下面讨论以不同速度运动的扰动点源所发出的微弱扰动的传播图形。由前述可推知，扰动点源所发出的微弱扰动以音速向各方向传播。图11．2给出了四种情况，图上实线圆表示微弱扰动波波面的位置，图上数字“－1”、“－2”等表示几秒钟前运动的扰动点源所在的位置，例如，“－3”即表示3s前扰动点源所在的位置，0即表示扰动点源当前的位置。

①扰动点源不动的情况。此时，微弱扰动向各方向传播到整个空间，波面是同心球面，投影在平面上就成为圆，球心与扰动点源位置O重合，如图11．2（a）所示。

②扰动点源的速度u小于音速a的情况。此时，微弱扰动仍能向各方向传播到整个空间，但在扰动点源运动方向上传播得慢，而在扰动点源运动的反方向上传播得快，如图11．2（b）所示。

③扰动点源的速度u等于音速a的情况。此时，在扰动源运动方向，所有微弱扰动的波面叠合形成一个平面（包含扰动点源在内），它将未受扰动区与受扰动区分开，如图11．2（c）所示。这就是说微弱扰动的传播不可能超越运动着的扰动点源，即微弱扰动不可能传播到整个空间。

④扰动点源的速度u大于音速a的情况。这种情况与情况③类似，但受扰动的区域缩小了。此时，所有微弱扰动的波面叠合形成一个圆锥面，它将未受扰动区与受扰动区分开，如图11．2（d）所示。这个圆锥称为扰动锥（也称马赫锥）。马赫锥的母线就是微弱扰动波的边界线，称为边界波（或马赫波）。马赫锥以扰动点源为顶点。

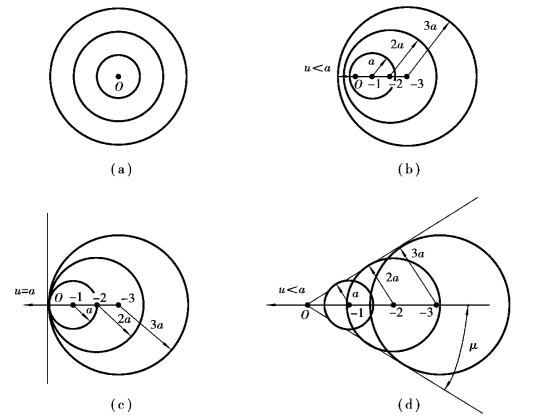
图11．2　微弱扰动的传播图形

为了便于今后讨论，需要知道流体运动而扰动点源不动的情况。根据运动相对性原理，上述情况②相当于流体以u＜a的速度流向不动的扰动点源，但流体运动方向与扰动点源运动方向相反的情况（此时坐标系取在运动的扰动点源上）。而相对于运动流体而言，扰动在流体运动方向上传播得快，传播速度为a＋u，在流体运动的反方向上传播得慢，传播速度为a－u。上述情况③相当于流体以u＝a的速度流向不动的扰动点源，但流体运动方向与扰动点源运动方向相反的情况。此时，相对于运动流体而言，扰动只能在流体运动方向（顺流方向）传播，不能在流体运动反方向（逆流方向）传播，而不动的扰动点源就是顺流方向与逆流方向的区分点。上述情况④相当于流体以u＞a的速度流向不动的扰动点源，但流体运动方向与扰动点运动方向相反的情况。此时，相对于运动流体而言，扰动点只能在顺流方向的圆锥内部传播，不能在顺流方向的圆锥外部传播，更不能逆流传播。上述圆锥顶角的一半，称为扰动角（也称马赫角），由图11．2（d）可得(www.daowen.com)

式中 M——马赫数。

马赫数是可压缩流动的一个重要参数，它等于流体流速与当地音速之比。由上面的讨论可知：流速大于或小于当地音速（即M＞1或M＜1）时两种流动图形截然不同。由流速的微小变化du或其他原因所引起的流体压强的微小变化dp，可以视为一种微弱扰动，而这种扰动在流速小于或大于音速的流体中的传播情况，由上面的讨论可知是完全不同的。

可以证明，在理想绝热（等熵）恒定流动中，M数是一个相似准则，故可按M的大小对可压缩流动分类如下：

M＜1　亚音速流动

M＝1　等音速流动

M＞1　超音速流动