任何一种气体都是弹性介质，有质量有弹性。在这种介质里，任何一个微弱的扰动必会自动地向四面八方传播，而且传播速度也有它一定的数值，其值只决定于介质的物理状态，与扰动幅度大小无关，也绝不因产生扰动的客体不同而不同。在空气或任一种气体里，这个数值确定的微弱扰动速度，在流体力学上就称为音速。在讨论可压缩流动时，流动速度大小同音速的比值，对流动有很大的影响，因此，音速是一个重要的概念。为了说明微弱扰动在可压缩介质内传播的机理，考察如下情况：

设在等截面直长圆管内充满静止状态的可压缩流体（视为连续介质），管内右端装一活塞，如图11．1（a）所示。若使活塞以微小速度dux向左运动，如此继续下去，这个过程以波的形式且以波速a向左传递，这就是微弱扰动波的传播过程，因此，通常称a为音速。在微弱扰动波波面通过之前的流体处于静止状态，压强为p，密度为ρ，而在波面通过之后，流体的速度由零变为dux，压强由p变为p＋dp，密度由ρ变为ρ＋dρ。微弱扰动波波面通过的区域称为受扰动区，而微弱扰动波波面未达到的区域称为未受扰动区。微弱扰动波波面就是受扰动区与未受扰动区的分界面。但是，图11．1（a）中的流场对于一个静止的观察者来说是非恒定的，这对研究是不方便的。如果围绕运动着的波面取一与波面同步运动的控制面，且观察者随运动控制面一起运动（图11．1（b）），则相对这个观察者来说，波面是静止不动的，而流体则始终以速度a流向波面，其压强和密度为p和ρ，始终以速度（a－dux）离开波面，其压强和密度为p＋dp和ρ＋dρ。这个观察者所看到的流体运动是恒定的。于是，关于一元恒定流动的基本方程就可应用于这个控制面。设所取控制面与x方向垂直的面积为A，则连续方程为

ρaΑ＝（ρ＋dρ）（a－dux）Α

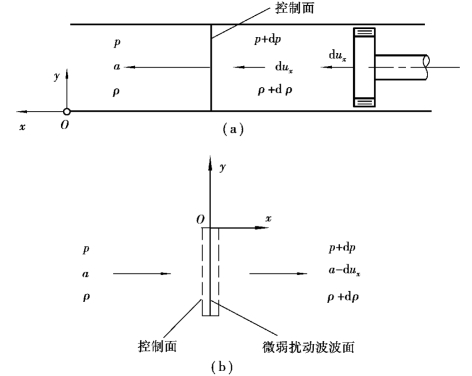
图11．1　微弱扰动波的传播过程

在忽略二阶微量后得

－ρΑdux＋aΑdρ＝0

或

动量方程（不计黏度影响）为

pA－（p＋dp）A＝ρaΑ［（a－dux）－a］

即

－Adp＝－ρaAdux

或

由式（11．1）和式（11．2）得

dp＝a2dρ

或(www.daowen.com)

若活塞向右运动，则由活塞向左发出的是压强下降的微弱扰动波。用类似的方法，可得与式（11．3）相同的公式。使流体压强产生微量增大的微弱扰动波称为微弱压缩波，反之，称为微弱膨胀波。当活塞向左运动时，由活塞向左发出的是微弱压缩波，而活塞向右运动时，由活塞向左发出的是微弱膨胀波。

为了求式（11．3）中的音速a，必须求式中右端的导数，而要求得此导数，必须确定此微弱扰动传播时所遵循的热力学过程。由于微弱扰动在传播过程中，流体的压强、密度和温度的变化无限小，因此可假定这个过程是等熵过程。

由热力学知，等熵过程方程为

于是，可求得

再由状态方程知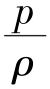＝RT，所以

由式（11．3）可知，当不同流体受到相同dp作用时，如果哪种流体的密度变化dρ较大，则在此流体中的音速较小；反之，如果哪种流体的密度变化dρ较小，则在此种流体中的音速较大，则不易压缩。当流体完全不可压缩，即dρ＝0时，则在此种流体中的音速a→∞。因此，音速可作为表征流体压缩性的一个指标。

再由式（11．5）可知，对于一已知的完全气体，音速仅是绝对温度T的函数。温度升高，音速增大；温度降低，音速减小。

式（11．5）中，R为气体常数，J／kg·K，k为绝热指数。对于常压下的空气，k＝1．4，R＝287J／kg·K，此时式（11．5）可近似简化为

a＝20．1T　（11．6）

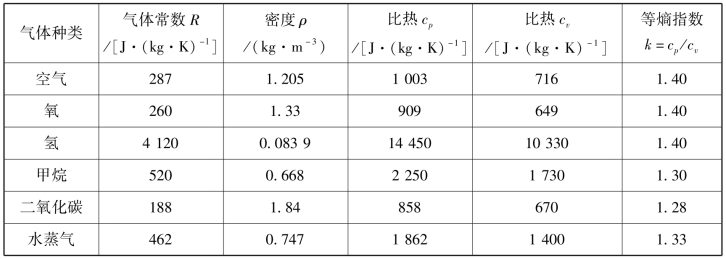
表11．1给出了常用气体常数。

表11．1　常用气体常数