对于实际流体绕圆柱体流动，如图10．11所示，出于黏性的关系，当Re＞20时，便发生分离，产生旋涡，在旋涡区的压强不能恢复到原来的势流时的压强，造成物体前后明显的压差，增加物体的绕流阻力，这时主要是压差阻力。

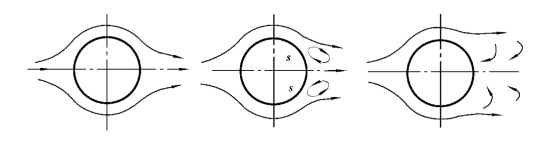
图10．11　绕圆柱体流动

由于理论上很难计算压差阻力，所以对于物体的型阻是通过试验来测定的。由于型阻与物体后面的流动能量的减少有密切关系，这就可以根据尾流的速度分布来推导型阻的大小，如图10．12所示。

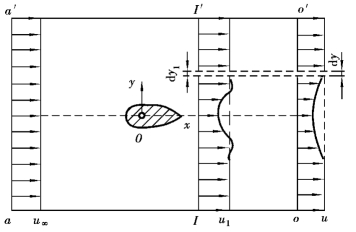
图10．12　用实验测定型阻

流体的速度u∞流过翼形体，在物体后方由于边界层影响，速度分布如图10．12所示。利用动量定理，取一包含物体的控制面aa′o′o，其中a⁃a′、o′⁃o平面垂直于来流，且距物体较远，以p∞和p0∞分别表示未被扰动的静压和总压，即

再假设平面o⁃o′距物体后面较远，以致物体在流场中引起的压力扰动对它的影响很小，这可以取o⁃o′面上的静压仍为p∞，记o⁃o′面上的速度为ux，总压为p0。

按动量守恒定律，对于恒定流动，在单位时间内由控制面沿x方向的动量的减少必须等于物体作用在流体上的力在x方向的投影（作用在a⁃a′、o⁃o′上的压强都是p∞，故x方向合力投影为零）。

从o⁃o′控制面流出的动量减去流进a⁃a′控制面的动量为

式中，h为x轴至a′⁃o′的距离。

从o⁃o′流出的流量与a⁃a′面流入的流量的差为

考虑到流体的连续性，通过a⁃o和a′⁃o′面的流量和应与此值相等，从而在x方向流入的动量为

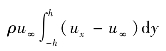
此外，假定h足够大，以至可认为那里的速度未被扰动，因此，总的动量减少应为

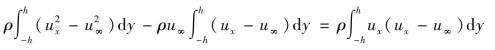
流体作用于物体上的力即型阻力为

式中，ux为未知数，反映离开物体后相当远地方的流体速度。由于实验只能在有限的距离内进行测量，为此需要将式（10．67）用近似的公式来代替。

在物体后不远处取垂直于流动方向的平面I⁃I′，如图10．12所示。在它上面的物理量标注以下标“1”，即在I⁃I′处流体速度为u1，静压p1，总压为p01。

在控制面I⁃I′和o⁃o′间取两条流线，由连续方程知：

ρux1dy1＝ρuxdy(www.daowen.com)

代入式（10．67）得

又因

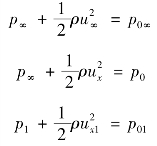
假定由控制面I⁃I′到控制面o⁃o′总压没有损失，即总压保持不变，p01＝p0则有

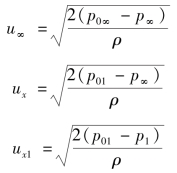
将上列各式代入式（10．68），得

由上式可知，沿控制面I⁃I′测得p01和p1的值就可以算出作用在物体上的阻力。

以上讨论了绕流阻力的计算问题，实际上，当Re继续增大，在Re为2×105左右，边界层转变为紊流，分离点突然后移，这时，虽然摩擦阻力由于紊流而增加，但由于压差阻力显著下降，发生CD的突然下降，出现所谓“阻力危机”的情况。此时，在物体后上下两侧交替地形成强烈的旋涡，并且这些旋涡有规则的排列，称为卡门涡街，如图10．13所示。

卡门涡街在大多数情况下都是稳定的，当Red≥5000时，由于尾迹中紊流加剧，不能清楚地看到卡门涡街。

卡门对这种涡街的实验研究发现，涡体脱落时，流体施加给圆柱体一个垂直于主流的周期性交变作用力，称为旋涡阻力（实质是儒可夫斯基升力）。交变的频率与涡流脱落频率相同。显然，脱落前后，圆柱体的绕流情况是不一样的，刚脱落涡流一侧，绕流受阻，侧面总压力较高，因而形成一个作用在圆柱上，方向总是指向刚脱落涡流侧面的作用力。这种方向交变的作用力，频率按下式计算，即

式中 St——斯特罗哈数；

d——圆柱体直径。

图10．13　卡门涡街

实验表明，St是Re的函数，而且有

卡门对这种上下两排旋涡（涡列）在不同排列情况下的稳定性进行了研究，研究结果表明，只有在两排涡列交错排列，且当两排涡列之间的距离h与同排中两相邻旋涡的距离l的比值为

时卡门旋涡才是稳定的。上式称为卡门旋涡的稳定性条件。

卡门旋涡的脱落频率很大，有时可以达到数百上千次每秒。如果这个频率与物体的固有频率相近时，就会引起共振。卡门旋涡脱落时还将使空气震动，发生声响效应，引起啸声和震动。野外的输电线在大风中发出的声音就是由卡门旋涡脱落而造成的。如果设计不当，潜水艇潜望镜有可能在大风中因谐振而破坏。1940年，美国华盛顿州塔可马吊桥被风吹毁就是这个原因。

工业上许多换热设备都由圆管做成，安装圆管的横向空间某一体积的气柱也有自己的声振频率，若设计不当，卡门旋涡脱落频率与气柱的声振频率相近时，就会诱发声波谐振，产生严重的噪声。上述频率一旦与管子的固有频率相同，更会造成设备的严重破坏。

设计者的重要任务就是要避免谐振发生，并尽可能减小绕流阻力。