上述研究的不可压缩流体绕零攻角平板流动的边界层问题,沿流动方向边界层中没有压强梯度,边界层外边界上速度相同。但在工程实际中,对流体机械和翼型、翼栅的绕流,以及管道内外的热交换时绕圆柱体管道的流动等,物体的壁面部是曲面。绕流时,边界层外边界上沿流动方向速度不断变化,边界层内的压强也将随之发生相应的改变。因此,曲面边界层又称为沿流动方向存在压力梯度的边界层。这种情况下,会产生边界层的分离现象。以下以图10.10所示的流过圆柱体的情况阐述边界层产生分离的机理。

图10.10 曲面边界层分离
若为理想流体,A、B为驻点,在E点有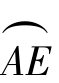
uE=umax=2u∞,pE =pmin
因为理想流体只有能量转变,无能量损失,故在段,![]() ,压能全部转变为动能,顺压梯度使质点加速;在
,压能全部转变为动能,顺压梯度使质点加速;在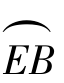 段,
段,![]() ,相反,动能转变为压能,但质点的动能刚好能克服逆压强梯度而达到B点,流体不会脱体。
,相反,动能转变为压能,但质点的动能刚好能克服逆压强梯度而达到B点,流体不会脱体。
对于实际流体,当流体以很小的雷诺数绕流时,与理想流体绕流几乎相同。流体在前驻点速度为零,然后沿圆柱对称向两侧绕流,在柱体前半部分是增速减压流动;在后半部分是减速增压流动,至后驻点汇合,速度又变为零。在流动中,由于流体的惯性力极小,整个流场都是层流,不产生分离现象,因此没有压差阻力,只存在不大的摩擦阻力。
当雷诺数增大后,物体表面的边界层变厚,但在固体壁面上,由无滑动条件ux=uy=0,边界层方程可变为

式(10.66)表明,靠边界处流体的速度分布曲线的曲率取决于压强梯度,符号随压强梯度的符号而改变。分成三种情况来讨论:
(1)AE段(https://www.daowen.com)
开始边界层很薄,与理想流动情况相差不大,随着边界层的逐渐增厚,压强降低,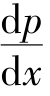 <0,流速增大,
<0,流速增大,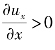 。由式(10.66)知,此时,
。由式(10.66)知,此时,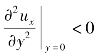 。而在边界层外缘,ux=ue,整个边界层内,
。而在边界层外缘,ux=ue,整个边界层内,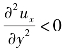 。可见,在这一段中,速度分布单调增加,称这段为减压(顺压)增速区。速度曲线沿x方向凸出,无拐点,不脱离。由于黏滞性影响,ue<2u∞。
。可见,在这一段中,速度分布单调增加,称这段为减压(顺压)增速区。速度曲线沿x方向凸出,无拐点,不脱离。由于黏滞性影响,ue<2u∞。
(2)ES段
在这一区域中,沿流动方向过流断面不断扩大,边界层外边界上压强增加,速度逐渐减小,即![]() 。由于增压减速,流动过程中质点要克服边界的阻力而消耗动能,以致不足以克服逆压影响,曲线沿x方向凹进,
。由于增压减速,流动过程中质点要克服边界的阻力而消耗动能,以致不足以克服逆压影响,曲线沿x方向凹进,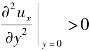 。而在边界外缘,ux=ue,在边界较远的某一点开始的一段距离,必有
。而在边界外缘,ux=ue,在边界较远的某一点开始的一段距离,必有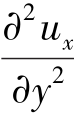 <0。这样,速度分布曲线上就出现了
<0。这样,速度分布曲线上就出现了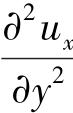 =0的拐点F,说明沿流动方向上逆压强梯度有阻止流动的作用,同时黏滞力的阻滞作用又不断消耗动能。沿x方向,
=0的拐点F,说明沿流动方向上逆压强梯度有阻止流动的作用,同时黏滞力的阻滞作用又不断消耗动能。沿x方向,![]() 逐渐减小,当达到某一S点时,质点动能耗尽,流速降为零,即us=0,此时,
逐渐减小,当达到某一S点时,质点动能耗尽,流速降为零,即us=0,此时,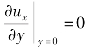 ,说明切于边界的速度分布曲线变为垂直于边界表面。此时,造成流体微团停滞不前,并在S点处堆积,边界层厚度迅速增大,S点就称为边界层分离点。也说明边界层分离是边界弯曲时,边界层内的逆压强梯度而引起的。
,说明切于边界的速度分布曲线变为垂直于边界表面。此时,造成流体微团停滞不前,并在S点处堆积,边界层厚度迅速增大,S点就称为边界层分离点。也说明边界层分离是边界弯曲时,边界层内的逆压强梯度而引起的。
(3)SB段
在S点,us=0,结果在某一SM线上,一系列质点的切向速度变为零,而在MSB区域内,由于逆压强梯度仍然存在,所以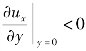 。由于主流的减速,所以边界层内的流体已不能从势流区获得能量补充。相反,在逆压作用下,壁面附近产生逆向回流,这股逆流徘徊于边界层与面壁之间,并排挤外流,迫使边界层脱体向外流移动。主逆流之间形成间断面(SM线),断面破裂后,形成一个个旋涡顺流而下,在物体后面形成尾流区,并伴随有巨大的能量损失,转化为物体的阻力(主要是压差阻力)。
。由于主流的减速,所以边界层内的流体已不能从势流区获得能量补充。相反,在逆压作用下,壁面附近产生逆向回流,这股逆流徘徊于边界层与面壁之间,并排挤外流,迫使边界层脱体向外流移动。主逆流之间形成间断面(SM线),断面破裂后,形成一个个旋涡顺流而下,在物体后面形成尾流区,并伴随有巨大的能量损失,转化为物体的阻力(主要是压差阻力)。
通过以上分析,得到以下结论:
①边界层的存在是尾流形成的先决条件,而尾流是边界层脱体的必然结果。
②在顺压区和逆压区中间必然存在有压强最低的点,此时,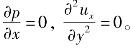
③边界层脱体的条件:脱体发生在逆压强减速区![]() 之后的区域,而在顺压区及零压区不会产生边界层脱体现象。
之后的区域,而在顺压区及零压区不会产生边界层脱体现象。
在工程上,为推后或避免边界层分离而引起绕流压差阻力,常将物体做成具有圆头和细长尾部的流线型。此外,紊流边界层比层流边界层不易分离,因为湍流的混合作用,将会延缓流体的滞止作用。最后,需要指出的是:在分离区,边界层方程式已不适用。因为在分离区边界层厚度变厚,δ/l不能认为是小量,所以破坏了边界层方程简化的前提条件。此时,边界层中的压力也不能再由主流中的压力来计算,而需要由实验来确定。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






