最简单的紊流边界层出现在零攻角的平板上，这类问题有一定的实际意义。例如，船体、机翼。透平机械叶片的表面摩擦力计算都与它有关。对零攻角平板的计算是最简单的，因为沿壁的压强梯度为零，所以边界层外边界上势流速度为常数，即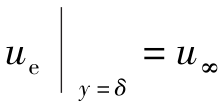。但在上述一些实际例子中，压强梯度通常不为零，但只要不发生分离，就与平板差别不太大，因此，研究平板的紊流边界层是计算各类物体无分离的摩擦力的基础。

现假定从平板前缘一开始（x＝0）就是紊流边界层，b为板的宽度。在计算平板层流边界层时，应用了两个补充方程。由于应用了层流时的牛顿内摩擦定律，在紊流时当然不适用，所以必须另找两个补充方程。普朗特假设：平板边界层内的紊流流动与圆管的紊流流动相同。即对于顺来流放置的薄平板，沿板长方向无压强梯度时，沿平板边界层厚度方向的速度分布规律与圆管沿管半径方向的速度分布规律相同。雷诺数不大时，可以采用1／7次方指数分布规律，即

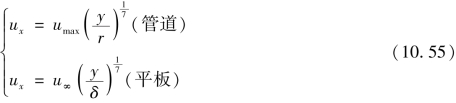
第二个补充方程是找切应力τ0和边界层厚度δ及u∞之间的关系式。仍与圆管流动相比拟，与式（10．55）相应的切应力表达式为

损失系数λ，对应1／7次方定律速度分布的紊流光滑区（4000≤Re≤105），采用布拉休斯公式，即

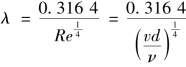
将上式代入切应力公式简化后得

式中，为平均流速。

对于管中紊流：

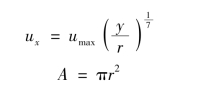
积分后得

所以

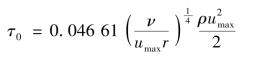
显然，管道中心y＝r处的流速umax与边界层外边界势流y＝δ处的速度u∞相对应，以此代替后，上式可变为

因为沿平板边界层内压强不变，即，故式（10．48）仍然适用，因此，将式（10．55）和式（10．57）代入式（10．48），得

积分后为

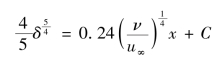
在平板前缘处，x＝0，δ＝0，所以C＝0，于是有

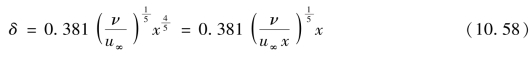
摩擦切应力为

可见，紊流边界层的厚度δ∝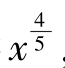，而层流边界层厚度δ∝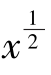，因此，紊流边界随x增长其厚度增加比较迅速。

平板一个壁面上的总摩擦力为

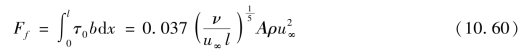
式中，Cf为摩擦阻力系数，即

(www.daowen.com)

上述推导过程中，采用了圆管紊流速度分布的1／7次方指数规律和光滑区阻力系数的布拉休斯公式，推得的结果有一定的适用范围，实验证明，在5×105≤Rel≤107范围内，式（10．61）求得的Cf值与实验数据十分吻合。但实际上，边界层起始总有一段为层流，当超过某xc长度后，在某断面处层流边界层开始转变为紊流边界层，转折点的位置将取决于外部流动的紊流强度和其他一些因素，由临界雷诺数Re＝u∞xc／ν决定。这种边界层称为混合边界层。由于层流段的存在，引起阻力的减少，如果假定转折点后紊流边界层还是像前缘那样（图10．6中的虚线部分），则可以计算阻力的减少部分。假定Ff为混合边界层的摩擦阻力，F″f是全部紊流边界层的摩擦阻力，F″foc是oc段的层流边界层的摩擦阻力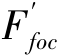，是oc段的层流边界层摩擦阻力，则

Ff＝F″f－F″foc＋F′foc

层流边界层时，宽度为b的平板前段的摩擦阻力，可以写为

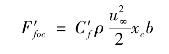
紊流边界层时，摩擦阻力为

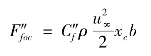
差值：

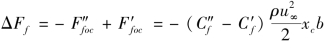
将等式两边各除以，这样由于层流段而产生的平板Cf的变化为

此处

A值与Rec的关系见表10．2。

表10．2　A值与Rec的关系

这样包含初始层流边界层的整个混合边界层的摩擦阻力系数为

由上式得出，层流边界层段越长，即层流边界层的转折点c离平板前缘越远，则平板的摩擦阻力就越小。当Rel＞107时，圆管内紊流速度分布是对数分布，可以设想在Rel较高时，紊流边界层内速度分布也为对数分布，即

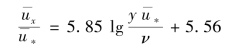
式中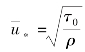， ——切应力速度。

由上式推导得到的平板流边界层摩擦阻力系数Cf与Rel的关系曲线如图10．9中的曲线③所示。普朗特和施里希廷对这条曲线拟合得到的经验公式为

这一计算公式的适用范围为106＜Rel＜109。

舒尔茨—格鲁诺根据对平板紊流边界层的大量测量结果，得到摩擦阻力系数的修正公式为

式（10．64）的曲线如图10．9中④所示。

考虑到初始段的边界层为层流，与推导式（10．62）一样，可得

A值与上述相同。图10．9中曲线①为层流边界层；曲线②为式（10．61）；曲线③为式（10．63）；曲线④为式（10．64）；曲线⑤为式（10．65）。分析图10．9中所示的曲线可以看出，随Rel增加，摩擦阻力系数都减小。但紊流边界层的Cf比层流边界层的Cf减小缓慢，在相同的Rel下，紊流边界层的Cf比层流边界层的Cf大得多，这是紊流中流体微团剧烈的横向混杂，产生紊流附加应力的缘故。因此，在工程上，对边界层进行人工控制，使绕流物体表面保持层流边界层，可以减小摩擦阻力。

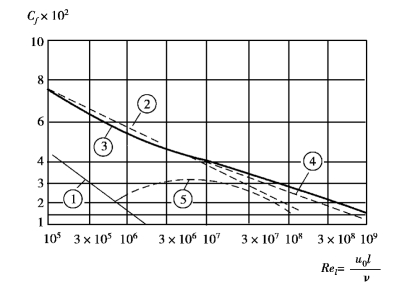
图10．9　平板紊流边界层计算曲线