得

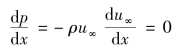
即在整个边界层中p＝常数，称为无压强梯度的边界层。

由式（10．47b）可知，此时动量积分方程可简化为

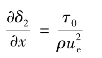
又因为流动恒定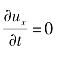，，对于无限宽的平板，流体作平面绕流，边界层厚度δ＝δ（x），因此，偏微分可改写为全微分，故上式又可写为

为了能对上式求解，需要先假设沿边界层厚度上的速度分布规律，这里假设以y的多项式表示，即

式中，a、b、c、…、m为待定系数，由边界层的边界条件确定。若假设为四次多项式，即

根据边界条件

①，所以系数a＝0；

②故有

③边界层外边界上，，于是

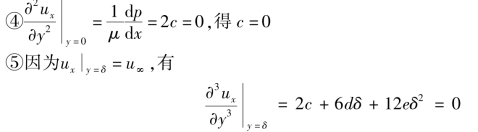
联解上述几个方程，可得

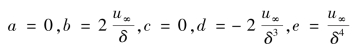
这样，层流边界层中速度分布规律为

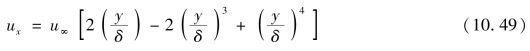(www.daowen.com)

因为是层流边界层，由牛顿内摩擦定律给出：

将式（10．49）、式（10．50）分别代入式（10．48）积分后得

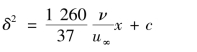
积分常数由边界条件确定：当x＝0时，δ＝0，得c＝0，所以，边界层厚度为

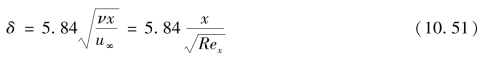
式中

由上式可见，平板层流边界层的厚度变化曲线是二次抛物线，δ随x增加而增大，但随流动雷诺数的增加而减少，流体黏性越大，边界层越厚。

将式（10．51）代入式（10．50），得到摩擦切应力为

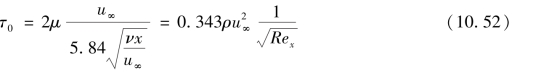
若平板宽度为b，平板面积A＝bl，则作用在微元面积dA＝bdx上的摩擦力为

dFx＝τ0dA＝τ0bdx

则作用在平板一侧表面上的总摩擦力为

摩擦阻力系数为

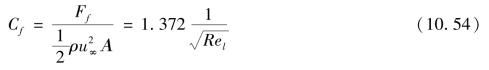
Cf与Re的平方根成反比。实验得到，当3×105＜Rel＜106时，可能为层流或紊流，主要取决于来流的状态、平板前缘形状和平板表面粗糙度。

若速度以不同次数的多项式给出，则上面从式（10．51）至式（10．54）中的系数有所不同。它们与布拉修斯（Blusius）给出的精确解的比较结果见表10．1。

表10．1　平板零攻角边界积分近似解与精确解的比较

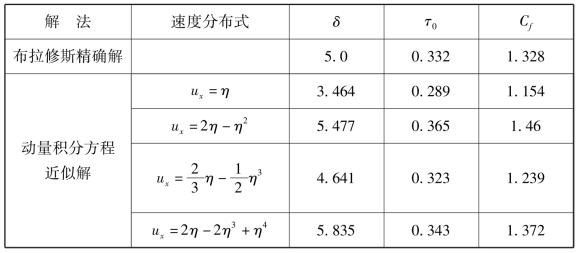
注：η＝y／δ。