虽然普朗特边界层方程比较简单，但是对于大多数工程问题，求解拟线性的偏微分方程仍十分困难，只有极少数的简单情况下才能求得精确解。为此，只有寻求近似的求解方法，其中冯·卡门（VonKarman）根据动量原理提出的动量积分方法，得到了广泛应用。

卡门于1921年用假设一个近似的边界层内的速度分布式代替真实的速度分布式，并使它仅仅满足动量积分关系式和边界条件，而并不要求每一个流体质点的运动都满足边界层方程，下面推导这个方程。

设流体沿二维固体边界作恒定流动（曲率很小），来流速度压强只沿流动方向变化，即p＝p（x）。在大雷诺数时，边界层厚度δ很小。取其中一微段ABCD作为控制体（单位宽度）来研究，考察质量的流进流出，如图10．7所示。

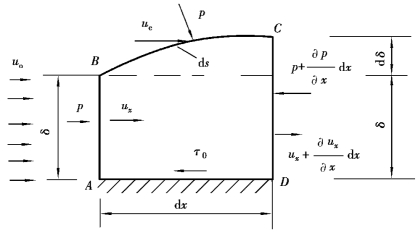
图10．7　边界层动量积分

dt时段流进的质量（AB面）为

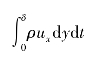
流出的质量（CD面）为

dt时段内的质量变化为

由连续方程知，它反映了BC面流进的质量。现在考察控制体ABCD内流体在单位时间内沿x方向的动量变化及受力关系。

作用力：设壁面曲率较小，则质量力（重力）在x向无投影。

表面力：压力和黏滞力。

①压力：

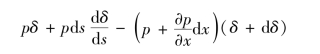
略去高阶微量得dt时段内的压力冲量

AD面的压力在x方向无投影。

②切力：BC面为外界流动。黏滞力可忽略，AB、CD面无投影，只有AD面有切力。设AD面单位面积上的阻力为τ0，则dt时段内的摩擦阻力冲量为

－τ0dxdt

现在考察动量：

①经AB面流入的动量

②经BC面流入的动量

③经CD面流出的动量

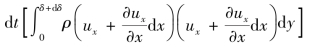
忽略高阶微量后，上式可化为(www.daowen.com)

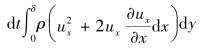
流出与流入的动量之差为

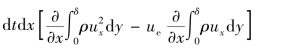
根据动量定理：单位时间内控制体上流体动量的变化等于外力的冲量之和。于是，有动量方程为

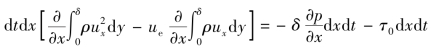
上式两边同除以dtdx得

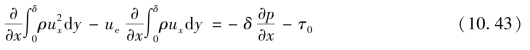
式（10．43）即为卡门动量积分关系式，由于对τ0未作任何限制，故对层流紊流都适用。

在方程中，ρ已知，可由势流理论求出，未知量有ux、δ、τ0三个，仍然不能求解，

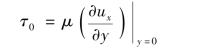
由边界条件和式（10．40）得但若已知ux＝f（x，y），并知道τ0与δ的关系，则对于给定边界条件即可对δ（x）求解。

若为不可压缩流体层流边界层，则有

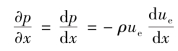
将上式代入式（10．43）得

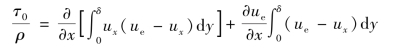
上式对y积分时，ue可以提出，故上式又可化为

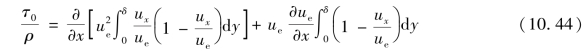
若令

式中，δ1、δ2分别称为排挤厚度和动量损失厚度，将在后面讨论。

此时，式（10．44）可进一步简化为

或

式（10．47）为卡门动量积分关系式的另一种形式。

动量积分方程虽然是一个近似关系式，但用它可以解决工程上很多与边界层有关的问题。

求解时的边界条件为

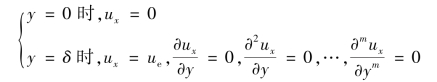
对于曲率较小的平面问题，速度可假设为y的多项式，此时，利用上面的边界条件（齐次），可求得边界层的厚度及绕流阻力。