利用边界层内流动特性，采用数量级比较的方法，可将N⁃S方程简化，得到边界层的运动微分方程式（或称普朗特边界层方程式）。

假设不可压缩流体作二维恒定流动，若将物体壁面的法向定为y轴，沿物体曲面流动方向定为x轴，因为边界层厚度很小，所以将δ放大时物体的曲率可以略去不计，x轴就变为直线，可以将绕任意曲面物体流动近似为绕平板的流动。当略去质量力时，N⁃S方程为

边界层简化的本质是依据数量级比较的概念，设被绕流物体的特征长度为L，来流速度为u0。简化假设：

①根据边界层y向厚度δ与x轴和速度ux相比很小，是个微量，即

②惯性力和黏性力同量级。

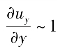又设δ的量级为ε（是个微量）即ε≪1。用符号“～”表示数量级相同，则δ～ε，而令x和ux的数量级为1，即x～1，ux～1，于是，在边界层流区有dy≪dx即由连续性方程知，故有。因而有根据第二假设有因为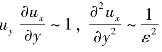，故而有ν～。将式（10．38）中ε以下的微量各项全部忽略，于是就得到普朗特边界层运动微分方程，即

由方程组中，可得到边界层的一个重要性质：沿边界层外法线方向压强不变，等于边界层外边界上的压强，即p＝p（x）。这一性质有十分重要的实际意义，因为边界层外流体作有势流动，所以边界上的压强分布p（x）可以由理想流体伯努利方程求得，又因为p与y无关，所以

在边界层外边界上，由势流的伯努利方程：(www.daowen.com)

故有

因为，所以在边界层内部有

式中，ue为势流区中的速度。这样，方程组（10．39）即可简化为

求解普朗特边界层方程的边界条件为：y＝δ处，ux＝ue，在壁面上y＝0处，ux＝uy＝0，由（10．41）式中第一个方程得到

如果势流速度ue的分布已知，根据上述方程组和边界条件就可以求解恒定二维边界层流动。

需要说明的是，在应用边界层方程时，一定要注意假设条件。当x向长度很小时，就破坏了假设条件，因此，对于边界层前缘部分，方程不能适用。

边界层微分方程式是边界层计算的基本方程式，但由于它是非线性的，即使对于形状很简单的物体的绕流，求解仍有一定困难。