（1）应力与变形速度（应变率）的关系

在材料力学中应力与应变之间存在一定的关系，这一关系由胡克（Hooke）定律所表达。在第1章中，曾讨论过牛顿内摩擦定律，这一定律相当于固体力学中的胡克定律，即

式中为剪切变形速度（即角变形速度）。式（10．3）可以推广到三元流动场合。根据流体微团运动分析可知，xOy平面上的角变形速度可表示为

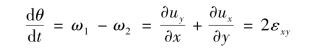
则

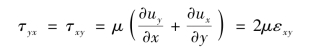
同理，对其他两个平面yOz和zOx上的切应力，也仿上进行分析，可得

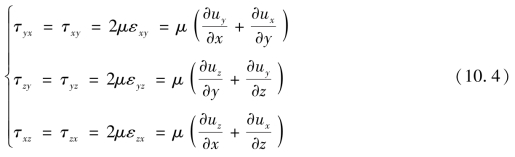
式（10．4）即为黏性流体中切应力的普遍表达式，称为广义牛顿内摩擦定律。它们说明切应力τxy、τyz、τzx分别与剪切变形速度（或角变形速度）分量εxy、εyz、εzx有关，而不是像胡克定律那样，与剪切变形有关。

实际流体运动时，由于黏性作用，不仅对剪切变形有影响，产生切应力，而且对流体微团在运动中发生的伸、缩等线变形也有影响，产生附加法向应力p′xx、p′yy、p′zz这一附加法向应力分别与流体中不考虑黏性效应（即应变率为零的情况）的动压强p相加，就可得黏性流体中各轴向的压应力，即

式中，p取负号是因为压强和图10．1中的正应力方向相反。

必须注意，法向附加应力p′xx、p′yy、p′zz可以是负值压应力，也可以是正值拉应力，这要视线变形是压缩还是拉伸而定。

由于切应力与法向附加应力在物理本质上都是黏性变形所产生的应力，因此，可以仿照切应力的广义牛顿内摩擦定律给出，附加法向应力等于动力黏度μ与两倍线变形速度的乘积，即

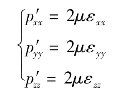
由流体微团运动分析理论可得

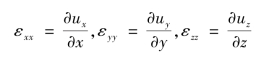
故可得到法向附加应力的表达式，即

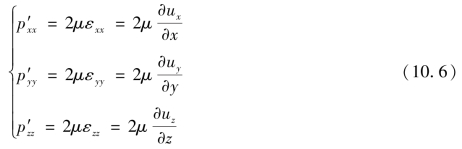
将式（10．6）代入式（10．5）可得

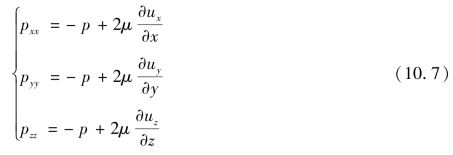
式（10．7）可看出，由于线变形速度不同，使得各个方向上的法向应力不相等。将式（10．7）中的三个方程相加，得

若定义：(www.daowen.com)

式中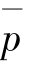，称为黏性流体中的平均动压强，它等于给定点行任意三个相互垂直微元面上法向应力的算术平均值。因此有

对于不可压缩流体

所以

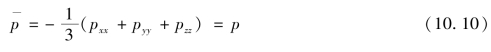
式（10．10）说明，对于不可压缩黏性流体，其流体动压强就是平均动压强。若微元六面体的边长dx、dy、dz趋近于零，这时，pxx、pyy、pzz变成黏性流体中A点上的三个法向应力，它们各不相等，但其算术平均值的动水压强p则不随方向而变，即黏性流体中的动水压强只是空间坐标和时间的函数。

对于平行流动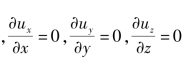所以有

pxx＝pyy＝pzz＝－p

（2）N⁃S方程

对于不可压缩黏性流体，若满足广义牛顿内摩定律，将已得到的式（10．4）和式（10．7）代入式（10．2）得

假设动力黏度不变，则上式可化为

对于不可压缩流体，等式左边第四项括号内等于零，并注意到μ／ρ＝ν，故有

同理

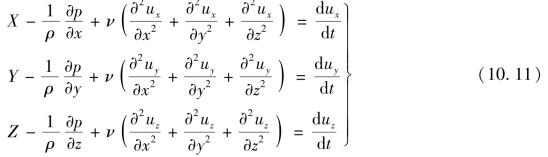
利用拉普拉斯（Laplace）算子代入上式有

式（10．12）也可写成向量形式，即

式（10．11）、式（10．12）或式（10．13）都可以称为不可压缩黏性流体的运动微分方程式，又称纳维——斯托克斯（Navier⁃Stokes）方程式（简称N⁃S方程）。

与理想流体欧拉运动微分方程式一样，它包含有四个未知数：p、ux、uy、uz，配合连续方程，从理论上，方程封闭，即有解。若为理想流体，则ν＝0，方程就化为欧拉运动方程式。若流体静止，则ux＝uy＝uz＝0，就变为欧拉平衡方程式。因此，N⁃S方程是黏性液体运动的基本方程，方程更具有普遍意义。