理想流体没有黏性作用，流动中流体间或流体与固体间不存在剪应力，而只有压应力（正应力）。并且可以证明，同静压强一样，理想流体中任一点的动压强在各方向上的大小也都相等。对于实际流体，情况就完全不同。由于实际流体是有黏性的，它阻抗流体质点的形状改变。因此，实际流体中，不仅出现了阻碍运动的摩擦切应力，而且也影响了法向压应力的性质。

现以作用在微小正交六面体流体微团ABCD（图10．1）为例，来说明压应力（即压强）和切应力的分布情况。

设流体微团的三条边长为dx、dy、dz，分别平行x、y、z轴，A点的坐标为（x，y，z）。因为所取的六面体无限微小，可以认为同一作用面上各点具有相同的应力。

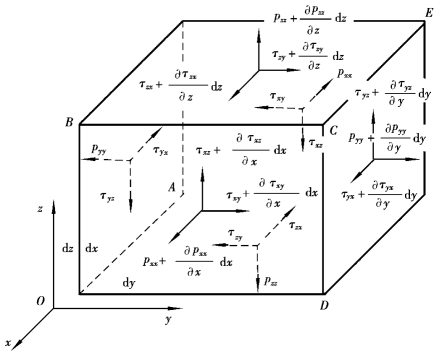
图10．1　流体中的应力

由于黏性的存在，六个面上都存在着表面力，且与作用面并不垂直，每个面上任意点的表面力总可以分解为法向压应力和切向剪应力。假设压应力在外法线方向为正，而过A点的三个平面上的切应力方向与坐标轴方向相反，由切应力性质知，通过C点的另外三个面上切应力方向与坐标轴方向相同，但由于位置不同，这三个面上的应力都有一个增量的变化。在直角坐标中，垂直于x轴的作用面AE上的任意点处的应力可以分解为

pxx、τxy、τxz

同样，作用在垂直于y和z轴的作用面上任意点处的应力分解为

τyz、pyy、τyz

τzx、τzy、pzz

其中，压应力p和切应力τ的角标，第一个表示与该应力的作用面相垂直的坐标轴；第二个表示与该应力的作用线相平行的坐标轴。这样，六个面上共18个应力。

若将六面体向A点无限缩小，这时三个作用面上的9个应力量就描述了A点的应力状态。因此，黏性流体中一点的应力由9个应力分量表示。但6个切应力分量之间，存在下列关系，即

证明如下：(www.daowen.com)

讨论受力的六面体处于任意运动状态。将作用于六面体微团上的所有应力，对六面体中心M而与x轴平行的轴线0⁃0取力矩，由于所有各面上的法向应力通过六面体中心，对M点取矩为零。质量力通过中心点M，不产生力矩。所取的力矩若以逆时针方向为正，顺时针方向为负，则表面力对该轴的力矩之和为

根据转动定律

式中 J——物体的转动惯量，对于平行六面体，J＝ρdxdydzdr2；

r——转动半径；

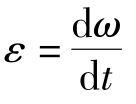——转动角加速度。

所以

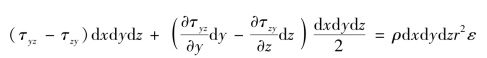
当dx、dy、dz趋近于零时，略去方程中四阶和五阶微量，有

同理可证

黏性流体中一点上的应力可以用6个独立应力分量表示，其中三个压应力，三个切应力。