（1）偶极子

偶极子是点源和点汇的叠加。如图9．12所示，将等强度的点源和点汇对称地放在x轴两侧，并互相接近，使a→0，但保持距离2a和强度Q的乘积为定值M＝2aQ，这种流动称为偶极流，M称为偶极矩。其流函数为

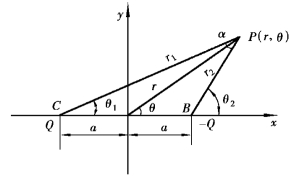
图9．12　偶极子的推导

从图中可以看出，设P（r，θ）为流场中任一点，P对源汇两点连接线PC、PB的夹角为α，则ψ可写为

对△CBP的θ1和α角按正弦定理有

当a→0时，α→0，sinα→α，r2→r，sinθ1→sinθ因此 αr＝2asinθ，将此代入式（2）得

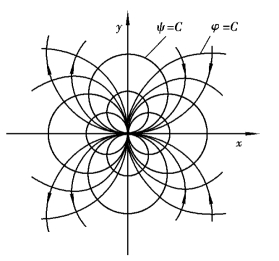
图9．13　偶极子流网

同理，可得

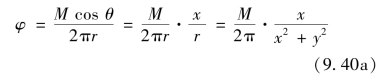
其中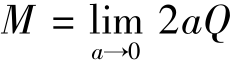，，M称为偶极子的强度。流线方程为

或

这是圆心在y轴的圆周簇，在原点与x轴相切，如图9．13所示。同理，势函数是圆心在x轴的圆周簇，在原点与y轴相切。偶极子在分析平行来流绕圆柱体的流动时非常有用。

（2）均匀流中的源流

均匀平行流与点源叠加后所形成的流动称为二维钝体绕流，如图9．14所示。均匀平行来流速度为u0，点源位于坐标原点，将水平均匀流和源流叠加，则其流函数和势函数为

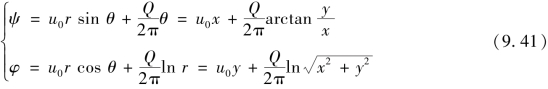
叠加后的流速为

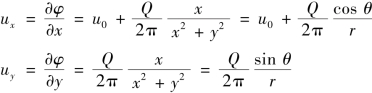
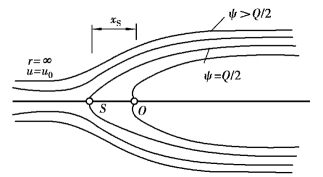
图9．14　均匀源流

其流场是绕物体前缘的流动，且叠加后的流速仍然满足r→∞处的边界条件。如图9．14所示，其驻点S点的位置（ux＝uy＝0）为

在通过驻点S的流线方程（边界轮廓线方程）为

边界轮廓线的渐近线方程为

（3）源环流

流体既有旋转又有径向流动，称为源环流。水泵蜗壳内的扩压流动属这种情况，但不是叶轮流道内的流动，如图9．15所示。其势函数和流函数为：

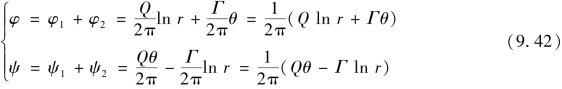
零流线方程为

表明流线是对数螺旋线，如图9．16所示。这种在半径为r1的内圆周到半径为r2的外圆周的流动，从内向外流速不断减小，而压强则不断增大。离心泵蜗壳中的扩压流动，就是依据这个原理而设计的，其径向和幅向流速为

这样，ur和uθ的比值保持不变，而且

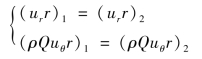
即断面1、2的动量矩相等，作用于流体的力矩为零，表明流体和固体没有力矩作用，流体内部没有动量交换，因此，不是流体机械旋转叶轮内部的流动。与源环流对应的流动是汇环流，多级离心泵和水力涡轮机中的导翼内的流动就是这种流动。

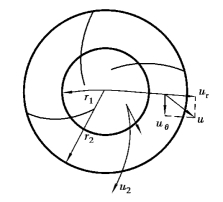
图9．15　源环流

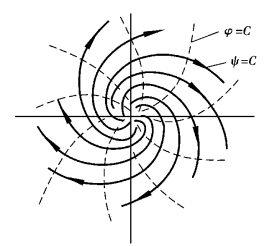
图9．16　源环流流网

（4）圆柱绕流

实际工程中经常遇到流体绕圆柱体的流动，各种冷却和加热设备多属于这种流动。圆柱绕流可分为两种情况：一种是无环量圆柱绕流，它是均匀流和偶极子的叠加；另一种为有环量圆柱绕流，它是均匀流、点涡和偶极子的叠加。

1）无环量圆柱绕流

无穷远处有一个平行均匀来流，圆柱半径为a，坐标原点（圆柱中心）处有一个偶极流，如图9．17所示。叠加后的流函数和势函数为

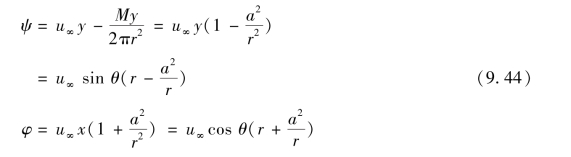
流场中任一点M处的两个流速分量为

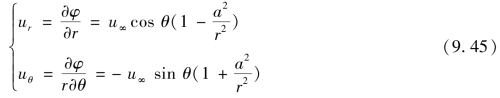(www.daowen.com)

由上面两式可看出，在r＝a的圆柱面上，零流线自无穷远处沿x轴到达A点，而后分两股沿柱面上下两半圆周流至B点汇合，在沿x轴向前流动到无穷远处，如图9．18所示。

当r→∞时，即距圆柱无穷远处，由式（9．44）得

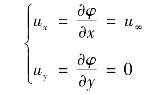
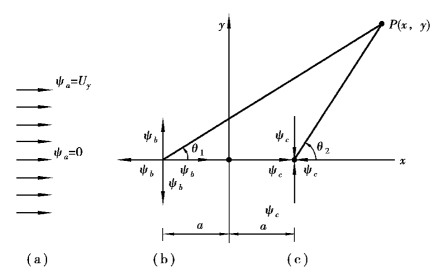
图9．17　无环量圆柱绕流

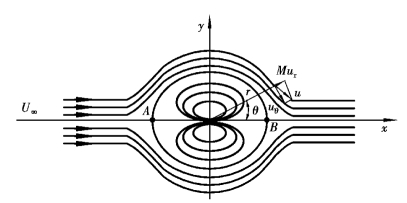
图9．18　无环量圆柱绕流

它满足平行均匀流。

在半径r＝a的圆柱上，有

它表明在圆柱表面上只有切向速度，而无径向速度，流动紧贴圆柱表面绕行，而不发生脱体现象。

在θ＝0°（B点）和θ＝180°（A点）——两驻点上，速度为零，在θ＝±90°处速度达到最大值，为原来的两倍。

柱面上任一点的压强，由伯努利方程得

因uθ＝－2u∞sinθ，代入可得

工程上常用量纲一的压力系数Cp表示作用在物体上任一点处的压强，其定义为

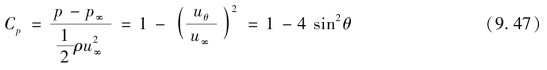
可以看出：沿圆柱面的量纲一的压力系数，与圆柱半径a及无穷远处的速度u∞均无关。

2）有环量圆柱绕流

对于有环流的圆柱绕流问题，其流场如图9．19所示。假设叠加一个顺时针点涡（Г＜0），此时，叠加以后的流函数和势函数分别为

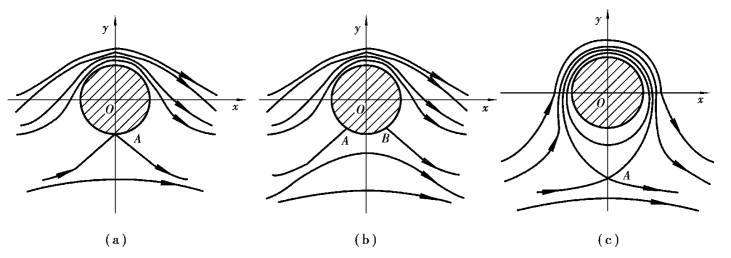
图9．19　有环量圆柱绕流

当r＝a时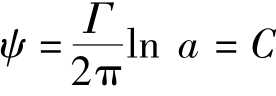，，即r＝a的圆周为一条流线。此时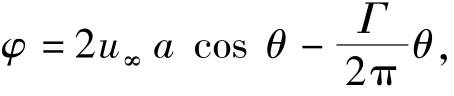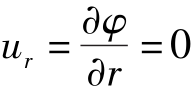，，，故只有沿圆周的切向速度，它满足圆柱绕流在圆柱面上的边界条件。当r→∞时，即距圆柱无穷远处，由式（9．48）得

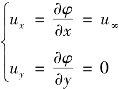
也满足圆柱绕流在无穷远处平行均匀流的边界条件。

流场中任一点M处的两个流速分量为

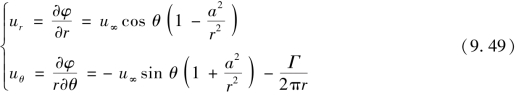
在半径r＝a的圆柱上，有

它表明在圆柱表面上只有切向速度，而无径向速度。从上式可以看出，在顺时针环流作用下，上部绕流与环流方向相同，速度增加而压强降低；下部绕流与环流方向相反，速度减小而压强增大。这就破坏了流线对x轴的对称性，使驻点A和B离开x轴，向下移动，如图9．19（a）所示。由于在驻点处速度为零，令uθ＝0，可求得驻点位置为

即θ角决定于Г和uθ之值。

若Γ＜4πau∞，则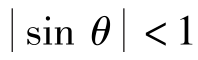，又因sin（－θ）＝sin［－（π－θ）］，则两个驻点将位于第三、四象限内，且对称排列，如图9．19（a）所示。在u∞保持不变的情况下，随环量Г的增加，两个驻点将向下互相靠拢。

若Γ＝4πau∞，则sinθ＝－1，此时两驻点合成一个驻点，位于圆柱最下端，如图9．19（b）所示。

若Γ＞4πau∞，则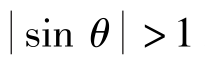，此时驻点已不在圆柱面上，而沿y轴向下移至某一位置。令式（9．49）中ur＝0，uθ＝0，可得到位于y轴上的两个驻点，一个在圆柱内，一个在圆柱外。这时，全流场由经过驻点A的流线划分为内外两个区域。外部为平行流绕圆柱的有环流的流动，而内部自成闭合的环流，如图9．19（c）所示。故此时只有一个在圆柱外的自由驻点A。

柱面上任一点的压强分布，可由伯努利方程求得

对于理想流体绕圆柱的流动，没有摩擦阻力，也没有压差阻力。

但在有环量圆柱绕流时，由于上下两侧的压强不等而形成一个升力，其计算式为

此即著名的儒可夫斯基升力定理。当Г＜0（顺时针），升力方向向上；当Г＜0（逆时针），升力方向向下。

日常生活中涉及升力的问题很多，例如，鸟类的飞翔，球类运动的旋转球，飞机的起飞、飞行和降落等。许多流体机械的工作原理，也与升力有关。

注意，本节所介绍的势流均为无界流场问题。

例9．5 图9．20为一种测定流速的装置，圆柱体上开三个相距为30°的压力孔A、B、C，分别和测压管a、b、c相连通。将柱体放于水流中，使A孔正对水流，其方法是旋转柱体使测压管b、c中水面同在一水平面为止。当a管水面高于b、c管水面Δh＝3cm时，求流速v0。

解 根据圆柱体表面流速分布公式，即

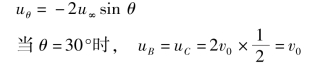
A、B两点能量方程为

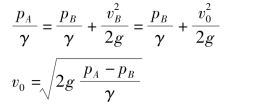
当

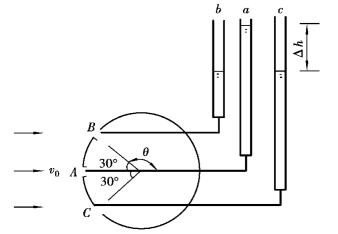
图9．20　圆柱形流速测定装置