（1）均匀流

流场中各点速度的大小和方向均相同，即ux＝a，uy＝b，a、b为常数。

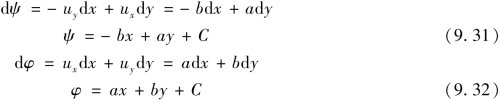
均匀流流网如图9．8所示。

（2）源或汇

无限平面上流体从一点沿径向均匀地向各方向流出，称为点源，如图9．9所示。点汇图9．10与此相反。

图9．8　均匀流流网

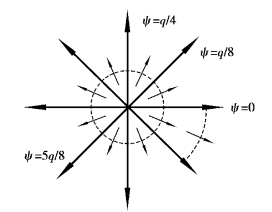
图9．9　点源

点源和点汇的流动都只有径向速度ur，将源点（或汇点）放在极坐标原点处，则

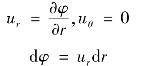
由连续性条件，通过任一圆柱面的流量应相等，其单宽流量为

或

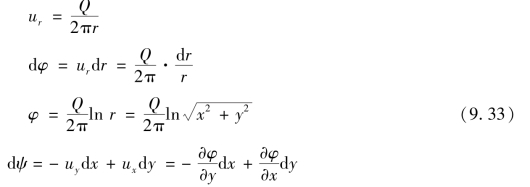
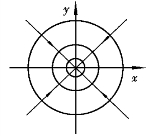
图9．10　点汇(www.daowen.com)

由式（9．33）和式（9．34）可知，其流线是通过圆心的射线，而等势线是同心圆。如图9．9、图9．10所示。

（3）点涡（环流）

设有一半径为r0的无限长圆柱，以ω绕其中心作旋转运动，周围流体将被带动作旋转运动，如图9．11所示。此时，会产生诱导速度，试验和分析证明，诱导速度与半径成反比，即

K为常数。当r＝r0，u＝r0ω，由此得K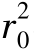＝ω

故有

u的两个分速

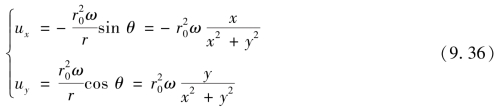
速度环量

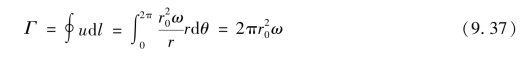
速度分布又可写为

其势函数和流函数为

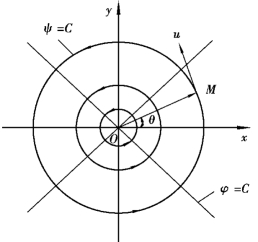
图9．11　点涡

Γ方向为逆时针方向为正。由式（9．39）可知，与点源或点汇相反，此时流线是同心圆，势函数是通过圆心的射线，如图9．11所示。与点源比较可以看出，只要将Q换成Γ即可，当然，环流的流函数多了一个负号。

点涡流场是一种除涡核心奇点外处处无旋的流场。在实际情况下，流动有旋的涡核心区具有一定的尺度。例如，河道或渠道中的立轴旋涡、有压管道上游容器淹没深度较小时产生的立轴旋涡，大气中出现的气旋及龙卷风等，都可以由点涡模型来描述。