①对平面有势流动，流函数满足拉普拉斯方程。

②平面流动中两条流线间通过的单宽流量，等于两条流线的流函数之差，如图9．5所示。

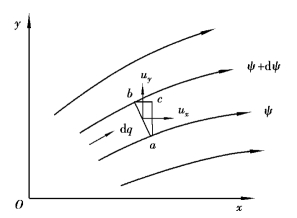
图9．5　流函数的性质

或

流函数与流线的区别：对于二维两者相同，对于三维，没有流函数，但流线存在。

求流函数：

注意：流函数积分时与路径有关。

③流函数和势函数的关系为

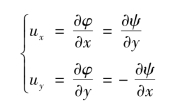
上式称为Cauchy⁃Riemann条件。

A．对于二维势流，φ和ψ均满足

Laplace方程，即

即φ和ψ是一对共轭调和函数。

图9．6　流网

B．等势线（φ＝c）和等流函数线（ψ＝c）正交，即

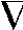φ·ψ＝0（9．30）

根据上面的性质，可以绘制出流网，如图9．6所示。

例9．3 三元不可压缩流场中，已知(www.daowen.com)

ux＝x2＋y2＋z2

uy＝－（xy＋yz＋zx）

且已知z＝0处，uz＝0，试求流场中uz的表达式。

解 由连续性方程式：

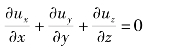
可得

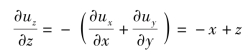
上式积分得

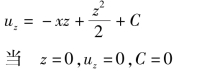
故可求出

例9．4 已知平面不可压缩流场的速度分量为：ux＝2x，uy＝－2y，试求其势函数和流函数。

解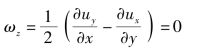

故此流动无旋，存在势函数φ，且有

积分得

又

满足二元连续性方程，存在流函数ψ，且有

积分得 ψ＝2xy＋C，其流网如图9．7所示。

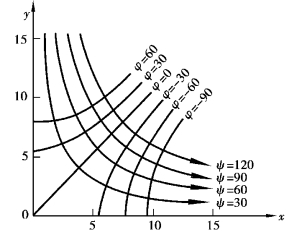
图9．7　流网