（1）涡管强度保持性定理

有旋运动的一个重要的运动学性质是：在同一瞬时，通过同一涡管的各截面的涡通量相等，称之为涡管强度保持性定理。这一定理可用下式表示，即

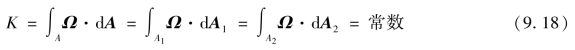
证明如下：

在某一瞬时取一涡管段，如图9．3所示。这段涡管的表面面积A包括截面A1、A2和侧面A3三部分。因而通过这一封闭曲面的涡通量为

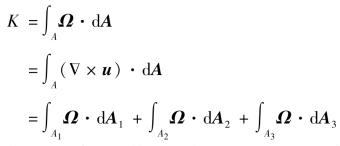
根据涡管的定义，涡线总是垂直于涡管的法线，因此，上式右边第三项为零；在截面A1上涡向量与截面的外法线方向相反。因此，上式整理为：

运用高斯公式和涡量连续性方程式（9．14）得

式中，τ是封闭曲面所包围的体积。因此，得

或

(www.daowen.com)

此式即式（9．18），证毕。

对于微小涡管，可以近似地认为截面上各点的涡通量为常数，即

Ω1A1＝Ω2A2＝常数

由上式可见，微元涡管截面越小的地方，流体的旋转角速度越大。由于流体的旋转角速度不可能为无穷大，所以涡管截面不可能收缩为零。也就是说，涡管不可能在流体内部开始或终止，而只能在流体中自行封闭成涡环，或者终止于和开始于边界面，例如，自然界的龙卷风开始于地面，终止于云层。

（2）Stokes定理

根据斯托克斯公式：

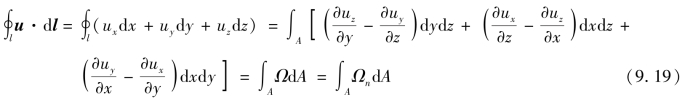
上式称为Stokes定理，定理给出了速度环量和涡通量之间的关系，即沿任意封闭曲线l的速度环量等于以该曲线为边界的曲面A的涡通量，即

Γl＝KA　（9．20）

（3）汤姆逊定理

汤姆逊定理指出：在理想流体的涡量场中，如果质量力有势，那么沿由流体质点所组成的封闭曲线的速度环量不随时间而变，即

上式称为汤姆逊（WilliamThomson）定理或开尔文（LordKelvin）定理。其本质与Stokes定理相同。

推论：根据斯托克斯定理，沿曲线l的速度环量等于通过以l为边界的曲面的涡通量。因此，速度环量不随时间变化也意味着涡通量不随时间而变。质量力有势的理想流体的流动，如果在某一时刻是有旋流动，在以前和以后也是有旋流动；如果在某一时刻是无旋流动，在以前和以后也是无旋流动。也就是说，这种流体的涡旋具有不生、不灭的性质。