欧拉运动方程是研究流体运动的基本方程之一，许多流动计算问题，例如机翼，流经流体机械（如泵和压缩机）的流道、管道和水利工程中的溢流坝等曲线边界的流动，需要精确地了解流速和压强的分布。理想流体的欧拉运动方程为解决这些实际流体流动问题提供了十分广泛的途径。

理想流体欧拉运动方程是应用牛顿第二运动定律于运动流体推导得到的微分方程式，是欧拉于1755年提出的，所以称为欧拉运动方程。

如图9．1所示，在流场中取一微小直角六面体δxδyδz，它的中心点A（x，y，z）上的压强为p（x，y，z，t）。假定流体为理想流体，则作用在微六面体表面上的表面力只有法向作用力，而作用在六面体质心上的单位质量的质量力分量是X、Y、Z。如果质量力和表面力不能平衡，则此微小流体六面体必将产生加速度a，就x方向而言，根据牛顿第二运动定律∑Fx＝max，得

经整理并除以微六面体的流体质量ρδxδyδz，便得

图9．1　微小直角六面体

同理，得y和z方向的方程

这就是欧拉运动方程。式中的加速度分量可按式（3．13）展开，便得方程组，即

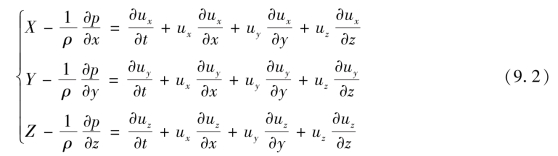
对于恒定流，有

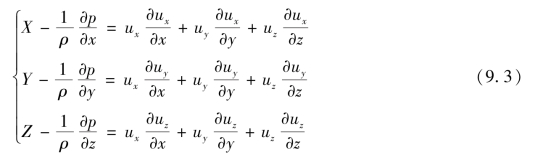
用矢量表示时，式（9．3）为

(www.daowen.com)

式中称为压强梯度，其值为

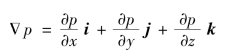
在场论中梯度用grad表示，故式（9．4）可写成

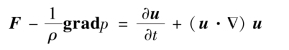
式中 F＝Xi＋Yj＋Zk为单位质量力矢量。

在一般情况下，作用在流体上的质量力X、Y、Z是已知的，对理想不可压缩流体其密度ρ为一常数。在这种情况下，式（9．2）中有四个未知数：ux、uy、uz和p，而式（9．2）中有三个方程，再加上不可压缩流体的连续性方程式，从理论上讲可解。

对于恒定流，应考虑到沿流线积分的条件，将式（9．3）中的三个式子分别乘dx、dy、dz，然后相加得

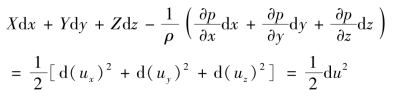
式中，若质量力有势，则左式中的前三项为力势函数的全微dW，左式括号中三项恰好为压强的全微分，因而有

或

对于不可压缩流体，ρ＝常数，式（9．5）积分得

这就是欧拉运动方程的伯努利积分。按照质量力性质不同，这个积分还可以有不同的形式。