考虑特征微分方程式（8．34）和式（8．35），此时已假设特征线方程近似为直线，因为常数，将式（8．34）和式（8．35）改写为

如图8．18所示，将上面两式分别沿特征线c＋和c－积分，积分限为ta、tb两个时间层，取一阶差分近似，即

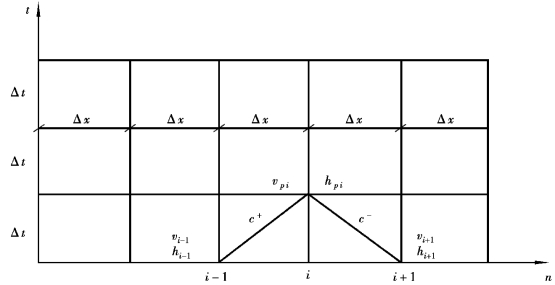
图8．18　水管水击特征线法的差分网格示意图

则式（8．55）和式（8．56）积分后分别有

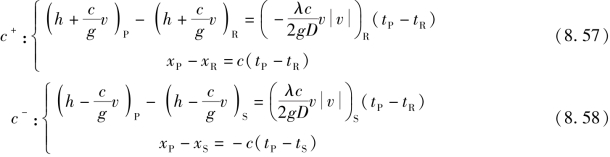
因xP－xR＝－（xP－xS）＝Δx，tP－tR＝tP－tS＝Δt，求解后一个时刻（网格中上一层）某P点的vP、hP时，可由前一个时刻（网格中下一层）两个位置R、S处的vR、hR和vS、hS值求得，采用网格坐标后，这时的特征线方程恰好形成了网格的步长关系，而且特征线也正好通过每一个网格点，因而可用网格坐标表示v、h的下标，vP、hP表示需要求的值，这样，联解式（8．57）和式（8．58），可得

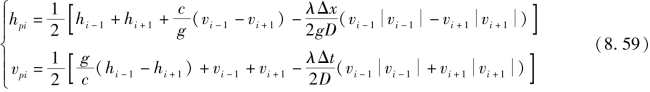
式（8．59）是求解网格内点的迭代关系式，其网格坐标可以这样来确定：将管道长度L分成N等份，并假设最大计算时间为tmax，则坐标与网格坐标及步长的关系有

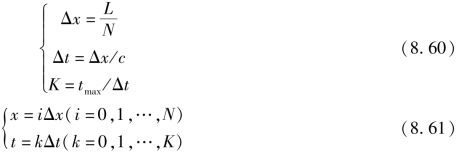
在X⁃t平面，按照式（8．60）和式（8．61）就可以建立一个规则的矩形网格坐标。

由前面的讨论可知：式（8．57）和式（8．58）分别适用于顺波和逆波的情况，因此，特征线法之所以优越，就在于这两个方程起到了协调边界方程的作用，而其他数值方法难以做到。考虑网格坐标后，这两个方程可写为

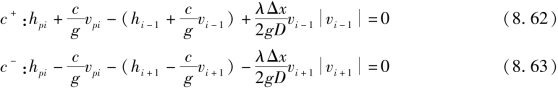
在求解管道问题中，有时用流量Q来代替v会比较方便，这时式（8．62）和式（8．63）变为

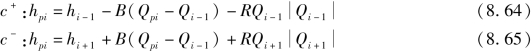
式中

A为管道面积。

在工程计算中，有时人们也很习惯采用量纲一的坐标，若令

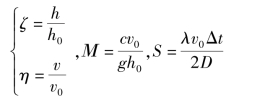
则式（8．62）和式（8．63）又可变为

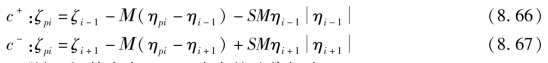
式（8．66）和式（8．67）联解后，其内点ζpi、ηpi式中的迭代解为

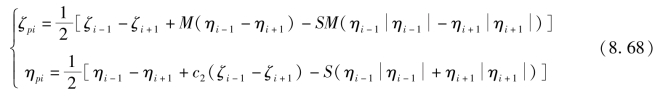
式中

若初始条件已知（k＝0），则由式（8．68）可以求出第一时间层（k＝1）内点i＝1到i＝N－1之间的解，而上游断面i＝0，下游断面i＝N应由边界条件和式（8．66）及式（8．67）联立求解，求解时一般设λ＝λ0＝常数。

定解条件：

1）初始条件

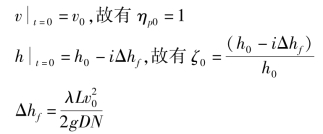
2）边界条件

这里仍假定为简单边界条件，即

①上游边界仍为大容器，则

hP0＝h0，故有ζP0＝1

根据前面讨论知，上游边界符合c－，但此时i＝0，i＋1＝1，由式（8．67）得(www.daowen.com)

令

则有

故此时上游边界条件为

②下游边界仍为阀门启闭调节引起水击，此时阀门开度可按时间的指数规律分布，即

且有

同理，下游边界符合c＋，但此时i＝N，i－1＝N－1，由式（8．66）得

令

则有

将上式代入关系式（8．72），得

解得

式中

在上述边界条件下，用VB语言编制计算程序如后，较为简单。

例8．3 有一简单管道水平放置，管径D＝0．9m，管长L＝1296m，上游端与一大水池相连接，其水头h0＝90．0m，管中最大流速v0＝1．1m／s，摩阻系数λ＝0．02，波速c＝1000m／s，阀门关闭时间Ts＝6s，管段N＝5段，其阀门关闭规律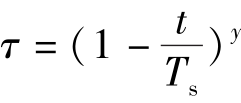，计算时间Tmax＝16s，关闭指数有y＝1和y＝2两种情况，求下游阀门断面水击压强的变化。

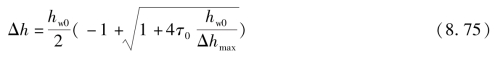
其中：

为阀门的初始开度，一般τ0＝1。

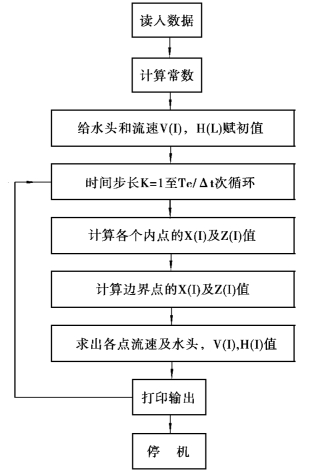
图8．19　计算框图

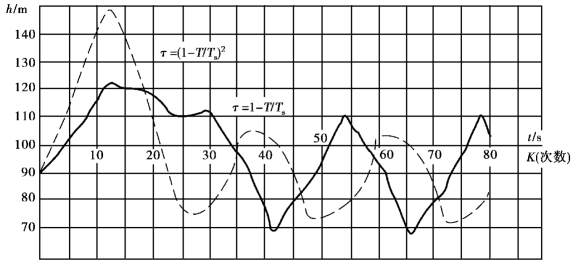
图8．20　计算所得水击曲线