水击压强计算的主题是确定最大（或最小）压强增值。对于直接水击，可以断定它发生的时间是在第一相末。对于间接水击，当阀门为线性关闭时，阿列维分析得出：它要么发生在第一相末，要么发生在末相，如图8．16所示。前者称为首相水击，后者称为末相水击。

图8．16　间接水击

（1）定解条件

与时间相关的微分方程的求解必须给出初始条件和边界条件配合求解——称为定解条件。对于不考虑摩阻影响的短管水击，如图8．17所示，其初始条件为

图8．17　短管水击

边界条件：

上游设为大容器，则

下游设为阀门：

阀门的启闭可视为一个孔口，通过水力学原理可以推求阀门的流量。设阀门相对开启度（初始流通面积为A0）为

通过阀门的流量在t时刻可近似写为

式中 μ0——流量系数，可视为常数；

Qt、At——t时刻通过阀门的流量与流通面积；

h ———t时刻通过阀门断面处的水头值。

管道中最大流量可写为

将式（8．41）除上式两端得

取量纲一变量，令

则式（8．41a）可变为

阀门的启闭规律：

假定阀门是线性关闭的，这时可分为两种情况：若阀门关闭时间为TS，则有

①直接关闭

②阀门部分关闭

若初始开度为τ0，末了开度为τe，则任意时刻t时的开度为

第k相的开度τk为

当ktr≥Ts时，τk＝τe

（2）水击压强计算

设顺行水击波C＋在t1时刻传到断面B，在t2时刻传到断面A，则式（8．38）可写为

反之，如逆行波在t1时刻传到断面A，t2时刻传到断面B，则有

采用式（8．42）的量纲一的变量后，上面两式可变为

式中

式（8．45）和式（8．46）称为水击的联锁方程，配合定解条件，即可求解。

1）第一相末水击

当阀门线性关闭时，应用逆波联锁方程式（8．46）可求出水击波由下游断面A传至上游B的压强与流速的关系。此时的时间t为O～L／c，即0．5相的时间。

按

此时已知

由此求得

再由B点0．5相的参数，应用顺波方程式（8．45）求A点1．0相的参数，即

式中：代入上式可求得第一相末水击压强计算公式，即

式（8．47）是当阀门关闭时，第一相末的水击压强增值的计算公式。若阀门不是关闭，而是由τ0开启至τ1时，第一相末水击压强下降值计算公式为

若为直接水击：

①阀门完全关闭

此时：τ1＝0，按式（8．47）有

或

式（8．48）和式（8．4）相同。

②阀门部分关闭

此时：τ1＝τe，同理可求得

式（8．49）和式（8．10）相同，这也说明直接水击时，最大水击压强必定发生在第一相末，并且可用简单公式计算。

2）间接水击时最大水击压强的计算(www.daowen.com)

间接水击时，最大压强可能为首相末，也可能为末相水击。用上面类似的方法，可求得B点1．5相末的关系式，再求A点2．0相末的关系式，结果为

逐次推算得第n相末及（n＋1）相末的计算公式如下，即

将上面两式相减，并考虑到

可得

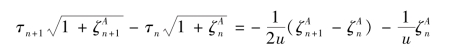
由图（8．16b）所示可知，当相数很多时有，由此上式可写为

设：则有

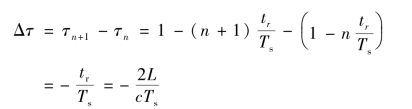
代入上式得

令：

则由上式可解出

若为阀门开启，则末相水击压强（最小）计算式为

例8．1 一压力引水钢管，管长L＝600m，管径D＝2．4m，管壁厚度δ＝20mm，作用水头h0＝200m，阀门全开时管中流速vm＝3m／s，阀门为针阀控制，Ts＝1s，试求下列情况下阀门处的水头：①初始开度τ0＝1，终了开度τ＝0；②初始开度τ0＝1，终了开度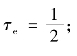③初始开度τ0＝0，终了开度τ＝1。

解 按薄壁钢管水击波波速公式

在三种情况下均为直接水击，可按第一相末公式计算其水击压强。其计算常数为

2u＝cvm／gh0＝980×3／9．81×200＝1．48

①按式（8．47）知：（τ0＝1，τ1＝0）

Δh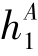＝－h0＝cv0／g＝2uh0＝1．48×200m＝296m

h＝h0＋Δh＝496m

②此时，由式（8．47）得

代入数据，解得

Δh＝0．5558×200m＝111．16m

h＝h0＋Δh＝311．16m

③此时τ0＝0，τ1＝1，当阀门开启时，首相末压强需按式（8．47a）计算，即

代入数据后得＝0．75

Δh＝0．75×200m＝150m

h＝h0－Δh＝50m

开启时由于负水击使其水头减小。

例8．2 某压力引水钢管，L＝316m，D＝4．6m，管壁厚度δ＝0．02m，如其作用水头h0＝38．8m通过的最大流量Q＝40m3／s，阀门完全关闭时间Ts＝6s，设开度为线性变化，求阀门断面最大水头增值。

解 水击波波速

相长，因Ts＞tr，故发生间接水击。此时，最大水击压强可能发生在第一相末，也可能发生在末相，需由计算判定。初始流速为

特征系数为

阀门线性关闭：

τ的下标表示相数。

利用公式：

解得

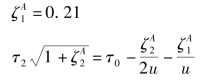
得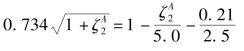

解得

＝0．33

第一相末水头增值为

Δ＝h0＝8．15m

第二相末水头增值为

Δ＝h0＝12．8m

从＞可知，此水击为末相水击类型。计算常数为

求得末相水击

故最大水击水头为

hmax＝h0＋Δ＝（38．8＋15．2）m＝54．0m

对于阀门终点任一相水击压强的计算，可编制简单的计算程序，若用k表示相数，其计算公式为

设阀门线性关闭，则

tk＝ktr

τk＝τ0－（τ0－τe）ktr／Ts