水击方程是一阶拟线性双曲型偏微分方程组，即最高阶偏导数线性，而且存在一组实特征线，沿特征线可将方程组简化为常微分方程，再运用数值方法进行计算。将式（8．21）的∂∂s用代替，并用L1、L2表示两个方程，即

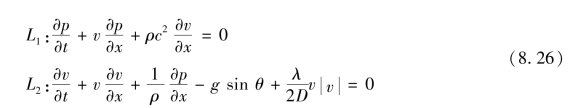
上述两方程用一任意的未知乘数λ1进行线性组合如下：

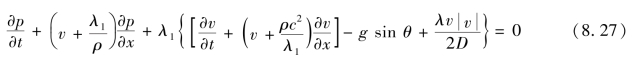
现设法选择两个λ1值，使得上式成为p、v的常微分方程，因为

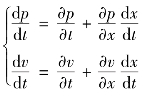
上式与式（8．27）比较，若满足下述条件，即

则式（8．27）可变为常微分方程，即

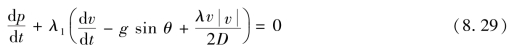
而由式（8．28）可解出

将λ1代入式（8．28）可得

式（8．30）是式（8．29）必须满足的两个条件，称式（8．30）为式（8．29）的特征线方程。

将λ1值分别代入式（8．29），并与式（8．30）组合，即可得到两个常微分方程组，用c＋、c－表示两个方向的特征线，则有

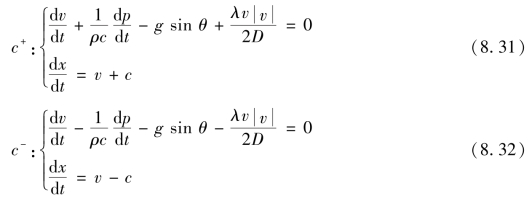
式（8．31）和式（8．32）称为水击方程式（8．21）的特征方程，表示水击方程沿特征线式（8．30）满足确定的微分关系式。这样，通过特征线方法将水击方程的偏微分形式确定转化成了常微分形式。

在实际使用时，式（8．31）表示发生水击时水击波（此时是顺波）由上游传至下游的特征关系；式（8．32）表示水击波（逆波）由下游传至上游的特征关系。

下面进一步讨论特征线方程的定义。式（8．30）在x⁃t平面上表示两簇曲线方程，如图8．13和图8．14所示。它们具有如下性质：

①在实际工程中，一般v≪c，故有

即其特征线斜率大于零，沿c＋满足式（8．31）。

即其特征线斜率小于零，沿c－满足式（8．32）。

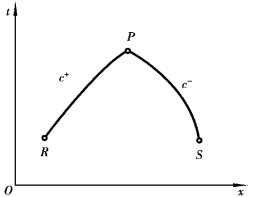
图8．13　特征线方程(www.daowen.com)

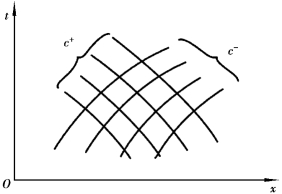
图8．14　特征线簇

②两特征线的交点汇于P，如图8．13所示，P点的vP、pP可由R，S两点的和vR、pR和vS、pS通过两特征微分方程求解得到。

③这里的x并不是任意断面的坐标，而是反映正反两个水击波波峰的运动位置，如图8．15所示。

④特征线方程的解构成一簇特征网，特征网的交点反映了任意时刻两方向相反的水击波波峰面的交界面，求解只能在这些交点上进行。

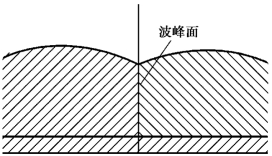
图8．15　水击波波峰

⑤对于工业金属管道，因｜v｜≪c，故特征线方程可简化为

即特征线方程近似为直线，这就给求解带来了很大方便。方程式（8．31）、式（8．32）是以水击压强p给出的，这时方程中出现了重力影响项－gsinθ同式（8．23）一样，若以测压管水头h表示时，则重力项也将消失。简化过程如下，先考虑式（8．31），因为此时dx＝cdt，而

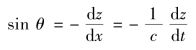
将此代入式（8．31），并将考虑进去以后，则有

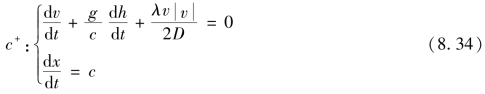
同理，对式（8．32），此时dx＝－cdt，而

同理，可以得到

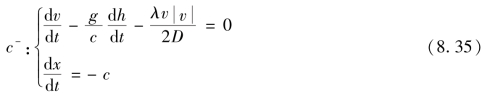
式（8．34）、式（8．35）是水击方程的特征方程的另一种形式，在实际计算时比式（8．31）和式（8．32）两式要方便得多。

倘若能将式（8．34）、式（8．35）进一步简化为如下形式，即

式（8．36）称为双曲型微分方程组沿特征线的黎曼不变量方程，方程表明沿特征线c＋和c－黎曼不变量r1、r2是个常数，则该方程就可以求出解析解。例如，式（8．34）、式（8．35）中若忽略摩阻项，则有

式（8．37）可以沿特征线求解析解，如图8．13所示，此时（在某一时间段上）有

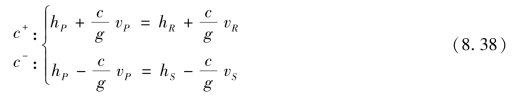
从而可解出

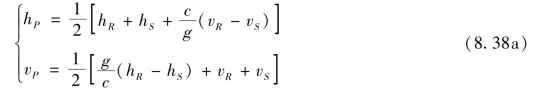
可以证明，式（8．38）即为短管水击忽略摩阻项后的解析解（这里用特征线法求解）。