管道中水击波波速的确定除了要考虑液体的压缩性之外，还要考虑管壁弹性的影响。下面来分析这一问题。

首先，分析质量守恒的连续性条件。当阀门突然关小时，阀门处压强首先突然升高，由于液体具有压缩性，其密度由ρ变为ρ＋Δρ，又因管壁具有弹性，其断面面积由A变为A＋ΔA，如图8．2所示。因此，在Δs段内液体质量的变化为

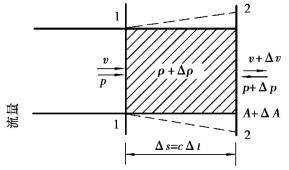
图8．2　考虑管壁弹性的水击

Δm＝（ρ＋Δρ）（A＋ΔA）Δs－ρAΔs

根据质量守恒原理，这一质量的增值，应该等于由上游1—1断面流进的质量减去由下游2—2断面流出的质量。如果流进1—1断面的流速为v，流出断面的流速为v＋Δv，则

Δm＝ρAvΔt－（ρ＋Δρ）·（A＋ΔA）·（v＋Δv）Δt

令上式与前式相等，忽略高阶微量，可得

ρΔAΔs＋ΔρAΔs＝－ρΔAvΔt－ΔρAvΔt－ρAΔvΔt

以ρAcΔt除以各项，并考虑水击问题中v／c≪1，故有

由上式可见，要求出波速c，还需要知道Δv与c的关系。为此，在既考虑液体的压缩性也考虑管壁的弹性的情况下，来分析Δs段液体的动量变化关系。

根据图8．2，Δs段液体在单位时间内动量变化沿流程s方向的分量为

［（ρ＋Δρ）（A＋ΔA）（v＋Δv）Δs－ρAvΔs］／Δt

作用在液体上的外力有：1—1断面上的压力P1＝pA，2—2断面上的压力P2＝（p＋Δp）（A＋ΔA）。侧壁上的压强平均值可近似地等于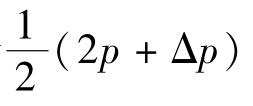，侧壁上的压力P在s

n方向的分量为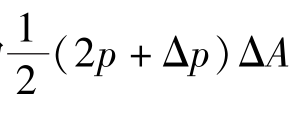。如不计阻力，则作用于Δs段液体上的外力在s方向的分量为

将以上关系代入动量方程，有

忽略高阶微量，得到以下与式（8．3）相类似的关系式，即

Δp＝－ρcΔv　（8．5）(www.daowen.com)

上式的负号表明Δp与Δv的变化方向相反。将式（8．5）代入式（a）得

上式右端第一项Δρ／ρ反映液体的压缩性，由第1章可知

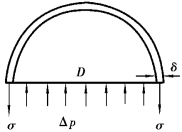
图8．3　管壁的弹性

右端第二项ΔA／A反映管壁的弹性。如图8．3所示，设圆管直径为D，管壁厚度为δ，管材弹性系数为E，由于增压Δp的作用，使D增加ΔD。如管壁应力为σ，则按材料力学中应力与应变关系有σ／（ΔD／D）＝E，又因均质薄壁圆管拉应力σ为：σ＝D·Δp／2δ，因此，可得

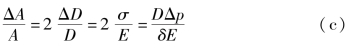
将式（b）及式（c）代入式（8．6），得

整理，得

式中 c0——忽略管壁弹性得到的水击波速（声速）；

K——液体的弹性系数；

E——管壁材料的弹性系数，钢管：E＝20．6×107kN／m2，铸铁管：E＝9．81×106 kN／m2；

D——管道内径，m；

δ——管壁厚度，m；

ρ——液体密度，kg／m3。

这就是考虑液体压缩性和管壁弹性的情况下管道水击波波速公式。

可以看出，水击波传播速度c与液体的体积弹性系数K、管壁的弹性系数E以及管壁的相对厚度D／δ有关。如果只考虑液体的压缩而将管道视为刚体，即E⇒∞，则c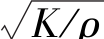＝＝c0，由此可见，不考虑管壁弹性的水击波，就是声波在液体中的传播速度。各种不同材料管道的弹性系数E可查有关手册。掺气以后的液流，由于其混合体积弹性系数大大降低，从而使水击波波速大为减小，可以从1000m／s降到300～500m／s。