油库利用自流进行收发油作业的情况是比较多的，当高架储罐无液体补充时，则在泄流过程中液面逐渐下降，即作用水头随时间降低，泄流流量也将随时间的延长而变小，形成不稳定流动。如果从高架储罐向低罐自流灌油，则高架储罐液面下降，低罐液面升高，罐间液面差随时间的延长而变小，也相当于作用水头变小，而流量也是逐渐减小的，这时关注的是泄流及排空作业时间问题。下面就分析这种变水头不稳定流的泄流原理以及泄流时间的计算方法。

（1）立式圆柱形容器中液体排空时间的确定

图7．33所示为一断面不变的柱形容器（如立式油罐），当水头不变时，其流量将由下式确定

当水头变化时，流量将随之变化，需用积分方法计算。

这时，可根据体积平衡列出微分关系式来进行积分。由于容器断面面积一般很大，可忽略惯性水头。

设在微小时段dt内，液面下降了dH的高度。令容器横断面面积为Ω，则由于液面变化引起的体积变化应等于同时段内排出的液体体积，即

－ΩdH＝Qdt　（7．49）

注意，在微小时段内可以认为是稳定流动，式中负号是由于随时间t增加。水头H要下降变小，即与时间成相反变化的缘故。将式（7．48）代入式（7．49）后，即可求得液面自H1降至H2所需的时间为T。这时作用水头为H＋z，z为定值，即

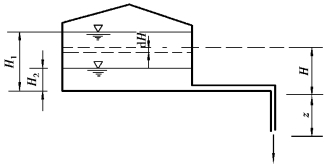
图7．33　自流不稳定泄流

取积分限由0到T及由H1到H2，积分后得

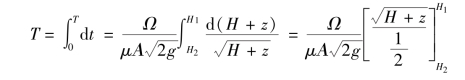
即

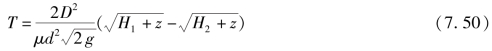
式中，A为泄油管出口面积。若油管直径为d，油罐直径为D，油罐装油高度为H，此时油罐泄油时的排空时间为

当z＝0时，有(www.daowen.com)

如果有并排n个管子同时泄油（例如，装油桶和灌装汽车槽车时），则A＝na（a为每个排油管出口的面积）。流量系数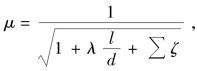根据实际情况确定。

（2）卧式圆柱形容器中液体排空时间的确定

如果容器断面是变化的（例如卧式油罐），则必须求出Ω随罐内油高h的变化关系，然后再进行积分。若罐为横卧圆筒，如图7．34所示，设油罐直径为D，长为L，罐内油高为h，罐底距泄油口高度为z，则Ω随h的变化存在下列关系。

其中，Ω＝Lx，由三角关系知，得

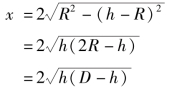
又知，H＝z＋h

故由式（7．49）得

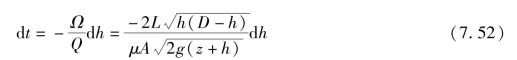
排空油罐所需时间为

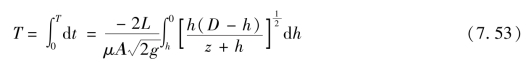
上式可采用数值积分（如高斯积分）求得结果。当h＝D时，也可以得到如下结果，即

式中，为随高度变化的一个函数，可由图7．35查得。

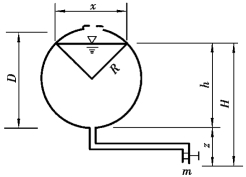
图7．34　变断面排空

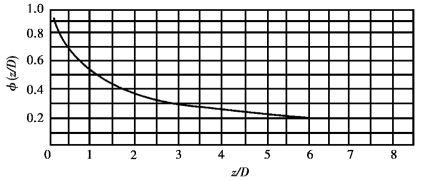
图7．35　函数的变化

由图7．35可以看出，在高差z不大的情况下，与高差z＝0相比较，自流泄油时间减短较快，而高差越大，泄油时间减短就越缓慢了。这是因为管线阻力增大的缘故，为有利于灌装，这时可以加大管径d，以减小管道阻力。