在器壁上开一个具有锐缘的圆形小孔，当液体流经该孔口时，液体与孔口壁面仅为线接触，所发生阻力只有局部阻力而无沿程阻力，这样的孔口称为薄壁圆形孔口，如图7．27所示。另外，如果孔口的直径时，称为小孔口。这时，可认为孔口的上缘深度和下缘深度相差不大，都等于形心处深度H，因此，认为沿整个孔口断面的流速是均匀分布。

液体流经孔口时，根据流线不能突然转折的特点，在孔口外约处形成一个最小的收缩断面c—c，该处的流线几乎为平行直线，为渐变流流动。设孔口断面积A，收缩断面积为Ac，则

图7．27　孔口

Ac／A＝ε

式中，ε称为收缩系数。

下面来推导孔口恒定出流的关系。

（1）自由出流

液体经孔口流入大气为自由出流，通过孔口形心取基准面，取1—1和c—c断面列能量方程，即

令

代入整理得

式中，称为流速系数。通常αc≈1，则

式中，ζc为孔口局部阻力系数。流速系数是一个小于1的系数。

孔口的流量为

式中，μ为流量系数，μ＝εφ。如果容器中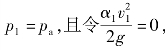则

Q＝μA2gH　（7．37）

式（7．36）及式（7．37）为孔口出流的基本计算公式。

（2）淹没出流

液体经孔口流入另一部分液体的液面上，称为淹没出流，如图7．28所示。此时，液体的流动情况与自由出流类似，所不同的是经过收缩断面后逐渐扩大。

图7．28　淹没出流

取通过孔口形心的基准面及1—1和2—2断面列能量方程，即

(www.daowen.com)

因为H1－H2＝H，故令

如果

式中，H为两容器中液面的高差。

比较自由出流和淹没出流的公式知，各项系数（μ、φ）均相同，计算公式的形式完全一样，但要注意式中H0或H的计算方法不一样，在淹没出流情况下，H为两容器液面的高差。同时，因为淹没出流孔口断面各点的水头均相同，所以淹没出流无“大”“小”孔口之分。

（3）收缩系数、流速系数及流量系数

孔口在壁面的位置对收缩有很大的影响。如果孔口离容器左右及底部壁面的距离l＞3d（d为孔口直径），则左右及底部壁面对收缩不发生影响，这种收缩称为充分收缩，如图7．29中孔口①那样。此时，射流具有最小的收缩断面。而在孔口②的情况下，器壁对收缩发生了影响，这种收缩称为不充分收缩，其收缩断面比充分收缩时的大一些。在图7．29中之孔口③，有的部分根本就不收缩，这种收缩称为部分收缩。因此，部分收缩的流量将大于其他以上两种收缩的流量。由实验得知：

薄壁圆形小孔口在充分收缩时，则

图7．29　孔口位置对收缩的影响

ε＝0．6～0．64

在不充分收缩时，则

ε＝0．63＋0．37（A孔／A壁）2　（7．39）

式中 A孔——孔口的断面积；

A壁——孔口所在断面的面积。

上式只有在A孔／A壁＜0．8时适用。

孔口的流速系数也由实验得出，为0．97。代入式（7．35）得孔口局部阻力系数ζc＝0．06。

圆形小孔口的流量系数μ如下：

充分收缩时

μ充＝0．60～0．62　（7．40）

不充分收缩时

部分收缩时

式中 n——孔口不发生收缩的那部分孔口边长；

x——孔口的周长；

K——经验系数，圆形孔口K＝0．128。正方形小孔口K＝0．152。