管网即为环状管道系统，是给水工程中应用较多的一种布置形式。管网计算一般是很复杂的，需用试算法或电算求解。

对于输水管道，还可用下述经验公式计算。

（1）经验公式计算

对于达西—魏斯巴赫公式，可写成

式中，S0称为比阻，即单位管长在单位流量（平方）的摩阻损失。

可知S0的单位s2／m6。

根据Ф·A·谢维列夫对使用两年的旧钢管和旧铸铁管的实验研究，当流速v＜1．2m／s时，管内水流为过渡区紊流，沿程摩阻系数为

当v＞1．2m／s时，水流为粗糙管紊流区，沿程摩阻系数为

将式（7．21）或式（7．22）代入式（7．19），得到计算输水管道hw的一般计算式为

式中，k为比阻的修正值，S0为粗糙管紊流时的比阻，即

当粗糙管紊流时，k＝1，过渡区紊流时比阻修正值为

将式（7．24）的比阻值S0和式（7．25）的比阻修正值k分别编制成表7．2和表7．3。由表7．2和表7．3，利用式（7．23）可简便计算旧钢管和铸铁管输水管道的摩阻损失。

表7．2　旧钢管和旧铸铁管在粗糙管紊流时的比阻S0值

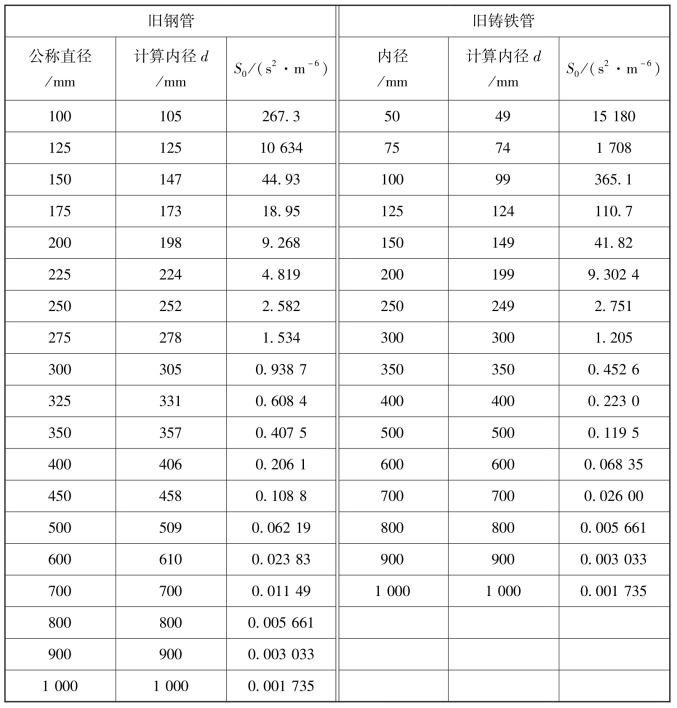
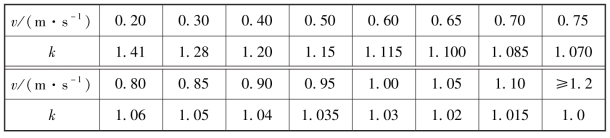
表7．3　旧钢管和旧铸铁管在过渡区紊流时比阻S0的修正k值

例7．13 给水管道为铸铁管，管径d＝400mm，通过流量Q＝126l／s，求L＝4000m管段的摩阻损失。

解 由表7．2查得，相应于d＝400mm的S0＝0．223s2／m6。因为

流动为过渡区紊流，从表7．3查得k＝1．03。因此，摩阻损失为

hw＝kS0Q2L＝1．03×0．223×（0．126）2×4000m（H2O）＝14．59m（H2O）

（2）环状管网的计算方法

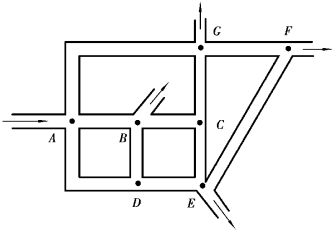
利用上述经验公式研究给水环状管网计算方法。环状管网由若干个闭合管环组成，如图7．11所示。

(www.daowen.com)

图7．11　环状管网

环状管网中，水流必须满足下列两个条件：

①根据连续性原理，流入每一个节点的流量必须等于流出的流量；

②沿每一个环路的压降代数和必须为零。

第二个条件说明在环路中任意两个节点间的压降必须相等，例如图7．11中的A和B节点间，无论是经过管AB还是经过ADECB都必须相等。因此，用解析法求解管网问题是不现实的，而要应用逐步渐近法。方法是假定各管道的流量，使得各个节点满足连续性方程，然后依次计算各环路的校正流量，以便使各个环路达到进一步的平衡。

摩阻损失用式（7．23）计算。为了书写方便，将其写成hw＝RQ2，这里R＝kS0L，若流动为粗糙管紊流，对每一条管道，R为常数，在计算环路之前，可事先确定。校正项由如下求得：

设Q0是任一条管道中假设的初始流量，即

式中，Q是正确的流量，而ΔQ是校正流量。于是对每一管道

式中，二阶微量（ΔQ2）可以略去。对于某个环路

式中，ΔQ之所以能从求和式中提出，是因为在环路的各条管道中它是相同的，而加上绝对值符号是考虑线环路求和的方向，通常规定假设沿顺时针方向的摩阻损失为正，逆时针为负。由上式求得管网中每一环路的ΔQ为

当按照式（7．26）将ΔQ用于环路中每一管道时，流向是十分重要的，也就是顺时针方向的流动时加ΔQ，而逆时针方向流动时减去ΔQ。

计算过程的步骤归纳如下：

①根据对管网的仔细分析，假定一个满足连续性方程而又是最佳的流量分配；

②在一个单元环路中计算并累加各管的净摩阻损失，同时计算由式（7．27）得到校正值，将此负值加于环路各管的流量中以校正；

③继续另一单元环路计算，重复②的校正过程。这样直至全部单元环路完了为止；

④根据需要再重复②和③步骤数次，直至校正值ΔQ足够的小。

在初设流量分配时，可根据每一单元环路中的每条管的实际R值大小设定，R值相对地越大，则Q较小。

例7．14 当给出图7．12简单环状管网中的流进和流出的流量时，试计算经过该管网的流量分配。

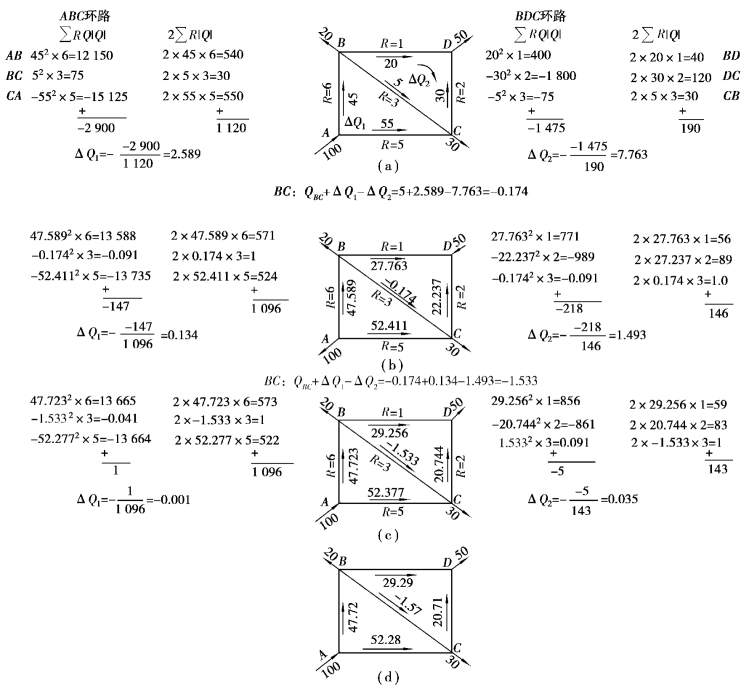
图7．12　环状管网流量计算

解 假定的流量分配如图7．12（a）所示。在图的左方是ABC环路的计算结果；在图的右方是BDC环路的计算结果。可以看出，只逼近试算三次，就得到足够的精确度。经过校正后的流量（图7．12（d））为

QAB＝47．723＋ΔQ1＝47．723＋0．001＝47．72

QAC＝52．277＋ΔQ1＝52．277＋0．001＝52．28

QBD＝29．256＋ΔQ2＝29．256＋0．035＝29．29

QCD＝20．744＋ΔQ2＝20．744－0．035＝20．71

QBC＝－1．533＋ΔQ1＋ΔQ2＝－1．533－0．001－0．035＝－1．57（与箭头方向相反）

环路单元更多的复杂管网，这种计算的难度就更大，但是，可利用电子计算机，这种计算就可获得迅速的答案。