油库中的收发油系统、城市供水管道、水电站的引水管以及其他供液气管道系统，分支管道是应用较多的布置形式，图7．9所示为一种最简单的分支管道系统。

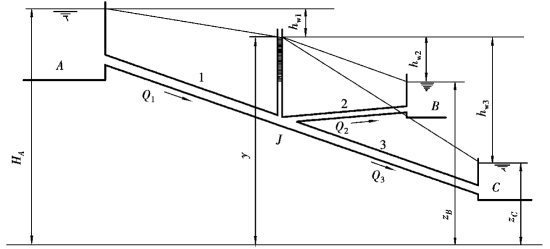
图7．9　分支管道

分支管道计算任务主要有：

①各装液容器（如图7．9中的容器B及容器C）的安装高程、管道长度及各种配件数量已知，在给定各支管流量条件下，确定管道直径及所需的作用能头HA。②供液容器A及装液容器的高程，管道长度及各种配件数量已知，在给定各支管流量条件确定管道直径。

（1）计算原理

在图7．9中，设支管2及支管3的流量分别为Q2及Q3，装液容器B及容器C的液位高程是zB及zC，在结点J设想装一测压管，测压管头zJ＋pJ／γ＝y。如果y高于zB及zC，则Q1＝Q2＋Q3，如果y低于zB而只高于zC，则容器B不但没有进液，反而与容器A共同向容器C供液，此时，Q1＋Q2＝Q3。

根据总流伯努利方程及连续性方程，对于y＞zB情况：

对于y＜zB

现按y＞zB＞zC的情况求解上述分支管道计算的两个基本问题。

①已知zB、zC、Q2、Q3及各管的计算长度L1、L2和L3，求d1、d2、d3及HA。

求解这类问题一般步骤是：

a．按给定的各干、支管流量，根据经济平均流速v初步确定各管管径d；

b．根据d，计算各管段的摩阻损失；

c．按式（7．15）求得HA。因为管径d是按经济流速确定，所以沿各支线方向计算得的HA不一定相等，此时取最大者；

d．根据确定的HA，校核调整支管直径。

②已知HA、zB、zC、Q1、Q2、Q3及各管段的计算长度，求各管道直径。

求解这类问题与第一个问题相似，此时按经济平均流速先确定干管直径，然后按式（7．15）求出各支管的直径。

例7．10 在图7．9中，已知Q2＝Q3＝50m3／h，zB＝30m，zC＝24m，L1＝220m，L2＝80m，L3＝150m，自流发出汽油（ν＝0．01cm2／s），求各管段直径及HA。

解 ①按经济平均流速初步确定各管径

由表7．1选取v＝1．5m／s，则

根据无缝钢管产品规格（附录表Ⅲ⁃1），初选

d1＝150mm（ϕ159×4．5）

d2＝d3＝100mm（ϕ108×4）

②计算各管段的摩阻损失（取Δ＝0．15mm）

Re1＝235785，λ1＝0．0210，hw1＝3．88m

Re2＝176838，λ2＝0．0231，hw2＝2．95m

Re3＝176838，λ3＝0．0231，hw3＝5．53m

③求HA

沿A→J→B HA＝zB＋hw1＋hw2＝（30＋3．68＋2．95）m＝36．83m

沿A→J→C HA＝zC＋hw1＋hw2＝（24＋3．88＋5．53）m＝33．41m

故取HA＝36．83m。

④校核调整管径

沿A→J→C所需的HA小于沿A→J→B，如果相差不大，可认为所初选的直径合适，如果相差太大，则应进行调整。一般情况下，只需调整所需作用能头较小的那些支线（A→J→C）。

现来计算管3的直径，即

HA＝hw1＋hw＋zC

hw3＝HA－hw1－zC＝（36．83－3．88－24）m＝8．95m

由式（7．9）得（注意H0＝hw3）

可选取d2＝94mm（ϕ102×4）的管子。实际上计算得的d3＝93mm与初选的d3＝100mm很接近。为了减少管子及其附件规格品种，便于施工，仍取d3＝100mm（ϕ108×4）为宜，但此时通过各支管的流量与给定的任务流量就有所不同。沿支线2变小一些，而支线3要大一些。

例7．11 在例7．10中求各支管的流量。

解 因各支管的流量未知，故干管、支管的摩阻损失也未知，需用试算法或图解法（见7．5节）解决。求解时首先假定结点J的测压管头y的高度，然后根据式（7．15）求得各管的流量。

设y＝32m，则

hw1＝HA－y＝（36．83－32）m＝4．83m

hw2＝y－zB＝（32－30）m＝2m

hw3＝y－zC＝（32－24）m＝8m

由式（7．6）

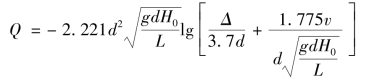
得

Q1＝112．31m3／h

Q2＝41．13m3／h

Q3＝60．48m3／h

这样，Q1＞Q2＋Q3，故所假定y太低，重新假定y＝32．5，则得

hw1＝4．33m， Q1＝106．20m3／h(www.daowen.com)

hw2＝2．5m，Q2＝46．13m3／h

hw3＝8．5m，Q3＝62．55m3／h

因为Q1－Q2－Q3＝（106．20－46．13－62．55）m3／h＝－2．48m3／h，说明流入结点J的流量小于流出的流量，再假定y＝32．4m，则得

hw1＝4．43m， Q1＝107．45m3／h

hw2＝2．4m，Q2＝45．17m3／h

hw3＝8．4m，Q3＝62．18m3／h

因为Q1－Q2－Q3＝（107．45－45．17－62．18）m3／h＝0．1m3／h，所以上述各管的流量便为所求。

（2）铁路装卸油系统的管道

图7．10所示为铁路装卸油系统输油管道示意图。卸油时油品同时经几个鹤管流入集油管aj，然后汇集流入吸入管OD经泵输送到储油罐中储存（有的油库有零位油罐，卸油时先虹吸自流到零位油罐，然后再用泵抽送到储油罐中）。装油时则方向相反，当有较大的地形高差时，即储油罐液面标高比发油鹤管出口较高时可以自流地发油。

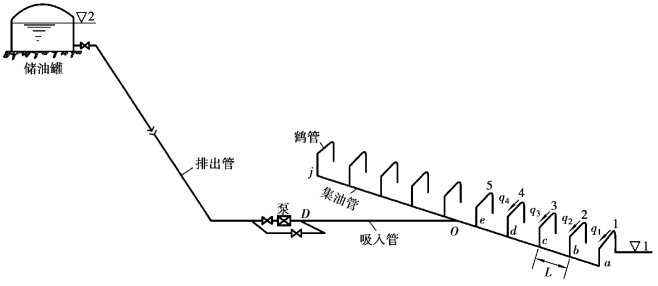
图7．10　铁路装卸油系统管道

铁路装卸油系统水力计算的任务是在给定各管段（鹤管、集油管、吸入管、排出管）的直径、长度、粗糙度和总流量的条件下，计算沿各鹤管的流量分配和管道系统的摩阻损失。计算时不考虑各油罐车中液面的高低不同，认为鹤管的出入口位于同一水平面上，并且压强都等于当地大气压。因此，计算时它类似于并联管道。只要各鹤管的流量求出，则各管段的摩阻损失就迎刃而解。虽然同一种油品的鹤管数很多，但是在装卸油时同时使用的鹤管数常常只有3～4个。因此，计算这类问题并不十分困难。

计算时，从集油管末端的鹤管1开始，因为所有的鹤管的出口都位于同一水平面上，所以由节点b流经鹤管2与由b流经集油管段ba、鹤管1的摩阻损失相等。同理，由节点c流经鹤管3与流经集油管段cb、鹤管2的摩阻损失也相等。以此类推，可分析出节点d、e、f等的摩阻关系。根据上述分析，如果hw表示鹤管中流动的摩阻损失，h′w表示两鹤管间集油管段的摩阻损失，则得

计算的步骤类似于并联管的计算方法：

①假定通过鹤管1某流量q′1。

②用假定的q′1算出h′wba及h′w1。

③因为h′wba＋hw1＝hw2，所以可算出q′2。

④根据q′1＋q′2算出集油管段cb的摩阻损失h′wcb，由式（7．17（b））算出q′3。

⑤同理，继续算出q′4、q′5等。假定流量Q沿鹤管的分配与流量q′1、q′2、q′3、q′4、q′5成相同的比

例，得

⑥用q1、q2、q3、q4及q5计算各相应的管段的摩阻损失，代入式（7．17）验算，当误差在3%以内时，认为满足要求。

例7．12 在图7．10中，设鹤管直径d＝100mm，计算长度L鹤＝25m，集油管直径d＝207mm，两鹤管间距L＝14m，同时用四个鹤管收汽油，总流量Q＝160m3／h，试求各鹤管的流量。

解 设鹤管及集油管的粗糙度相同，Δ＝0．15mm，汽油的黏度ν取1×10－6m2／s。

①假定q′1＝32m3／h

②由q′1计算h′wba及hw1

集油管段ba：Re′＝54675，λ′＝0．023，h′wba＝0．0055m

鹤管1：Re′＝113176，λ′＝0．0237＝0．0237，h′w1＝0．3875m

③计算q′2因h′w2＝h′wba＋h′w1＝（0．0055＋0．3875）m＝0．393m

由式（7．6）得

q′2＝0．0899m3／s＝32．37m3／h

④计算集油管段cb的摩阻损失

Re′＝4×（q′2＋q′1）／πdν＝4×（32．37＋32）／（π×0．207×10×3600）＝109981

λ′＝0．0211

h′wcb＝0．0206m

⑤计算鹤管3、4的流量q′3及q′4

h′w3＝h′wcb＋h′w2＝0．0206＋0．393＝0．414m

q′3＝0．00924m3／s＝33．26m3／h

同理，得q′4＝0．00975m3／s＝35．10m3／h

⑥计算实际通过各鹤管的流量

q1＝38．57m3／h

q2＝39．02m3／h

q3＝40．09m3／h

q4＝42．31m3／h

⑦根据q1、q2、q3、q4校核各管段摩阻损失是否满足式（7．17）（计算过程略）

节点b：

hwba＋hw1＝（0．00785＋0．556）m＝0．564m

hw2＝0．568m（误差0．7%）

节点c：

hwcb＋hwz＝（0．0293＋0．568）m＝0．597m

hw3＝0．599m（误差0．9%）

节点d：

hwdc＋hw3＝（0．0651＋0．599）m＝0．664m

hw4＝0．666m（误差0．3%）

上述计算结果，误差在千分之几以内，可见，此计算方法，精确度较高。