图7．2所示为一自流简单管道。它利用天然地形或人工修筑具有自流输液位差，液体从高储液库（如油罐、水池等）向低液位容器输送。由于储液库的横断面很大，自流时，液面变化很缓慢，可视为恒定流。管道出口，可以如图中那样流入容器的液面下，称为淹没出流，也可能流入大气，称为自由出流。以下按淹没出流情况研究其水力计算方法。

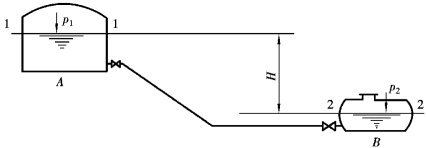
图7．2　自流简单管道

设两容器中的液面高差为H，管道长度及各种配件已知，则根据恒定总流伯努利方程

或

令等式左边

得

H0＝hw　（7．2）

式中，H0为上、下游两断面单位总能头差，称为作用能头。通常，管道两端容器中液面与大气相通，p1＝p2＝pa。同时，由于容器断面很大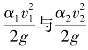，可以忽略，此时z1－z2＝H0＝H，则式（7．2）变为

H＝hw　（7．3）

式（7．3）表明，两断面间的作用能头H0全部用于克服该管段的摩阻而消耗掉了，表明能量的供与需相平衡。

因为，所以式（7．2）也可写为

为便于记忆，将常数π及g的数值代入得

式中 d——管道直径，m；

L——计算长度，m；

Q——流量，m3／s。

在应用式（7．4a）时，必须遵守上述规定的各量的单位。因为0．08266是一个含有单位的量（s2／m）。

利用式（7．4）或式（7．4a）可以求解管道输送能力计算的3个问题。

（1）求摩阻损失hw（或H0）

求摩阻损失即为求作用能头H0。例如，要确定水塔高度，高架油罐的安装高度便属于这类问题的计算。此时，Q、d、ν及Δ是给定的，利用式（7．4）直接解出。

例7．1 在图7．2中，已知流量Q＝150m3／h，液体的运动黏度ν＝0．1cm2／s，d＝150mm，计算长度L＝400m，Δ＝0．15mm，两容器液面上均为大气压强，求所需的安装高度H。

解

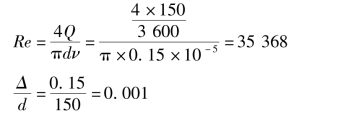
λ查莫迪图6．19得，λ＝0．025。如果用方程式计算，因为

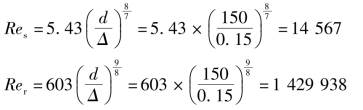
则Res＜Re＜Rer为紊流过渡区。

用式（6．62）计算

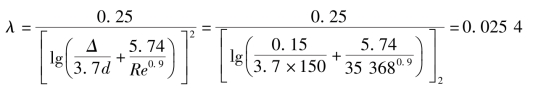
依式（7．1）或式（7．3），得

H0＝hw＝H

再根据式（7．40），得

（2）求流量

利用式（7．4a）求流量时，因为Q未知，则Re未知，因而流态及λ皆为未知，不能直接求出Q。为了确定它，可用下列步骤求解：

1）比较作用能头，确定流动形态

因为在d、L及ν已确定的情况下，从层流过渡到紊流的临界状态时，必定相应有一个临界作用能头Hc（即摩阻损失），根据层流时摩阻损失的计算公式（6．24）

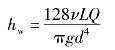
再根据雷诺数计算公式

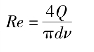
在临界状态时，Re＝Rec＝2300，由上述两个方程，求得不包含Q的临界作用能头，即

当H0＜Hcq时，流态为层流，H0＞Hcq时流态为紊流。

2）计算流量

若流态为层流，用式（6．24）直接求得Q；若流态为紊流，可按下述步骤试算。

①计算Δ／d值，查阅莫迪图（图6．19），可先假定一个λ概值（一般在紊流过渡区范围内选取），然后将其代入式（7．4a），第一次算出Q值。

②根据算得的Q值，计算雷诺数Re，再从莫迪图查出对应于Re的λ值，再代入式（7．4a），第二次算出Q值。

③根据步骤②算得的Q再计算Re及λ，如果λ值的头两位有效数字不变化时，则算得的Q值即为所求。

例7．2 汽油储油罐中液面与发油点容器中液面高差为150m，管长8．5km，管径d＝150mm，Δ＝0．15mm，汽油的运动黏度ν＝0．01cm2／s，两容器中液面均通大气，求自流发油流量。

解 ①比较作用能头，确定流态

由式（7．5）得

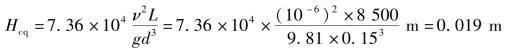
依式（7．1），得

H0＝H＝150m

有H0＝H＞Hcq，故流态为紊流。

②计算流量Q

因为，查图6．19，取λ＝0．021，代入式（7．4a）得

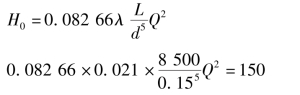
得

Q＝0．02778m3／s

根据所得的Q值计算雷诺数，即

查莫迪图得λ＝0．0209，再代入式（7．4a）得

Q＝0．02785m3／s

再用该流量计算雷诺数Re及λ，分别得(www.daowen.com)

Re＝236398

λ＝0．0209

可见，Q＝0．02785m3／s＝100．3m3／h为所求。

由上例看出，对于黏度近似于水的流体，其临界作用能头Hcq很小，工程实践中极少出现层流流态。因此，计算时可按紊流考虑，不必判断流态。

对于紊流流态的管流，可由柯列布鲁克公式（6．59）及式（7．4）推导出流量的显式公式。

由式（7．4）得

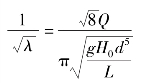
将代入式（6．59）并整理得

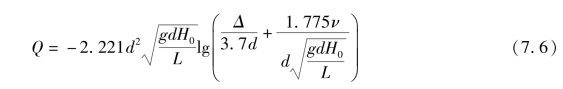
此式是由斯韦密和杰恩首先导出的，它在相同的Δ／d及Re值适用范围内和柯列布鲁克公式具有同样的精确度。

如将例7．2中各数据代入式（7．6），得

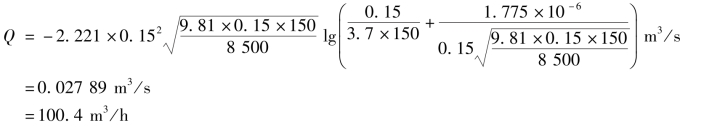
（3）求管径d

因为d未知，因而Δ／d及Re未知，λ不能求出，也不能由式（7．4a）直接求得d。此时，计算d的方法可按下述步骤进行：

1）比较作用能头，确定流动形态

因为在Q、ν及L已知的情况下，由层流过渡到紊流的临界状态时，相应也存在着一个临界作用能头Hcd。类似于（2）的推导，得到不包含d的临界作用能头的计算公式为

当H0＜Hcd时，流态为层流；H0＞Hcd时，流态为紊流。

2）计算d

若流态为层流，用式（6．24）直接求得d；若流态是紊流的，则按下列步骤试算。

①假定流动处于阻力平方区，初选管径。因为流动在阻力平方区时，λ与Re无关，将该区λ的计算公式（6．64）代入式（7．4a），整理后得

利用此式初步确定直径范围。

②求λ。按式（7．8）求得的管径d，计算Δ／d及Re，查莫迪图或用式（6．62）计算，求得λ。

③将求得的λ值代入式（7．4a）求得管径d。

④由③求得的d，重复②及③的步骤，直到当λ值的头两位有效数字不变时，即可认为满足要求。

通常只经过一两次试算即可满足，因为往往在选取下一个管径时要比计算得的管径要大一些的标准管径。

步骤①也可用光滑管紊流初选d，读者可以自行推导。

例7．3 一输油管道，已知H0＝54m，要求输油速度Q＝500m3／h，油品的运动黏度ν＝0．09cm2／s，管道计算长度为1650m，试选定管径。

解 1）比较作用能头，确定流动形态

根据式（7．7）计算临界作用能头，得

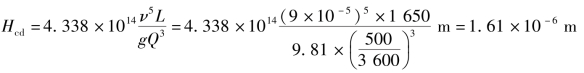
因为H0＞Hcd，所以流态为紊流。

2）计算d

①假定流态为阻力平方区，初选管径

取Δ＝0．15mm，由式（7．8）得

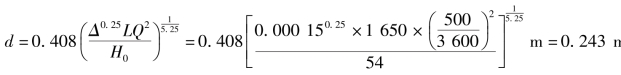
②计算λ

因为

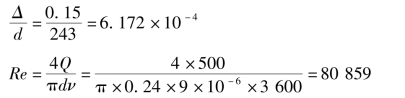
所以

③计算管径

由式（7．4a）得

④将步骤③算得的d＝0．253m重复步骤②及③，得

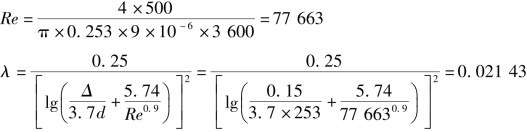
可见，算得的λ值与步骤②所得的λ值基本相等，则d＝0．253m为所求。但无缝钢管的标准直径中，并无此规格（见附录表Ⅲ⁃1），故决定选取ϕ273×7（“273”为外径、“7”为壁厚）的标准直径无缝钢管。斯韦密和杰恩通过用量纲一的关系和类似建立柯列布鲁克公式那样，得到紊流流态直接计算管径的经验公式，即

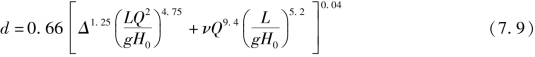
式（7．9）在下列范围内适用：

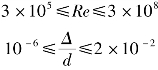
在这个范围内算得的管径d与按柯列布鲁克公式计算得的数值误差在2%以内。若将例7．3的数据代入式（7．9）得

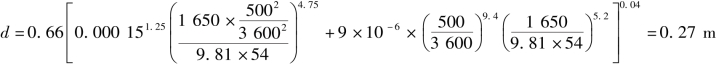
这个数值与用试算法计算的结果很接近，误差只有1．4%。

上述各种计算，虽然是针对自流情况，但是其计算原理对于用泵或风机输液或输气管道也是适用的。

例7．4 图7．3所示为离心泵输水。已知泵排出口压力表读数p1＝1．962×106Pa，容器B液面比泵出口高72m，管道直径d＝200mm的铸铁管，Δ＝0．3mm，长度l＝5km，水的黏度ν＝0．01cm2／s，求摩阻损失及流量。

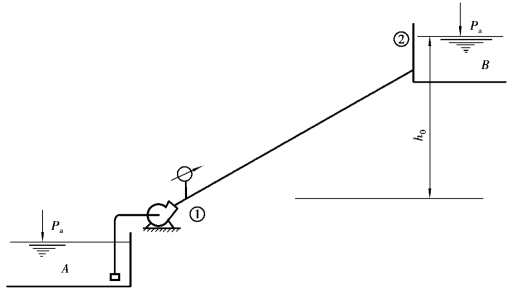
图7．3　离心泵输水

解 对泵出口断面①与容器B液面为断面②列总流伯努利方程，即

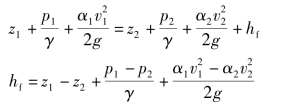
因为z1－z2＝－72m，p2＝0（表压强），按长管考虑

得

由式（7．6）得

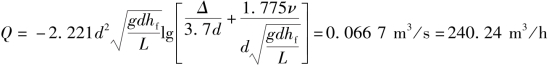
校核紊流阻力区域v，即

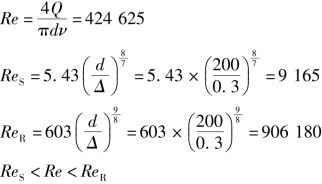
故所求流量正确。