除了层流运动能从理论分析推导得λ的计算公式外，工业管道紊流沿程摩阻系数计算公式都是半经验或经验性的，这方面的公式很多，这里介绍比较普遍采用的公式。

（1）光滑管紊流区

在光滑管紊流区时，沿程摩阻系数λ只与Re有关，与管道相对粗糙度无关，1913年伯拉修斯（H．Blasius）在总结光滑管紊流大量试验资料的基础上，第一个得到λ的显式计算公式，即

这个公式在满足式（6．56a）的条件下，在Re＜105与实验点非常吻合。如果Re＞105，则有所偏差，此时，用普朗特公式（6．50）计算，即

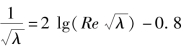
此式精确，但缺点是隐式公式，计算时需用试算法才能求出λ值。

苏联富兰凯尔根据他的研究得到与式（6．50）同样适用范围的显式光滑管紊流公式，即

这个公式与B·米勒（B．Miller）1937年提出的公式类似。所不同的是常数为－1．53，而不是－1．5。

（2）紊流过渡区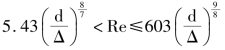

在紊流过渡区中函数式反映该区的λ的变化规律。它的具体经验函数式，由柯列布鲁克（Colebrook）1939年与怀特（C．M．White）合作，将普朗特光滑管紊流λ计算公式（6．50）及卡门粗糙管λ计算公式（6．51）机械地结合起来，得到过渡区紊流摩阻系数公式。简要过程如下：

式（6．50）可写为

式（6．51）为

注意上述两式自变数Re和的前面都有对数符号和相同的系数2，考虑到紊流过渡区公式应当有：当时，应该变为光滑管紊流公式，而在Re→∞时，则应当变为粗糙管紊流公式，而在紊流过渡区的λ是Re和的函数。因此，将上述两式简单地结合起来得到表示过渡区紊流λ的函数关系式，即

这就是柯列布鲁克公式。注意该式中，当雷诺数较小，相对于可以忽略时，式（6．59）就变成光滑管紊流摩阻系数λ的计算式（6．50）；当Re很大，相对于值可以忽略时，式（6．59）则变成粗糙管紊流摩阻系数λ的计算公式（6．51）。通常认为式（6．59）是适用于整个紊流区的综合计算公式。

图6．18　过渡区紊流尼古拉兹实验曲线与柯列布鲁克公式（6．59）沿程摩阻系数曲线比较

图6．18表示在紊流过渡区尼古拉兹人工粗糙管实验数据与柯列布鲁克公式（6．59）所得的结果的比较。应当注意到柯列布鲁克并不停止在式（6．59）的分析解上，他对各种形式的工业管道进行了大量试验，发现同一组管道都有相同的曲线，与式（6．59）非常接近。式（6．59）求解比较困难，莫迪（L．F．Moody）以式（6．59）为基础，绘制了一种较为简便地确定工业管道摩阻系数的曲线图，他将λ表示为相对粗糙度及雷诺数Re的函数的一种斯坦顿（Stanton）图，即阻力系数与雷诺数的重对数图，如图6．19所示。整个图线也分为5个区域，即层流区、临界区、光滑管紊流区、紊流过渡区和完全紊流粗糙管区（平方阻力区）。利用莫迪图确定λ值是非常方便的，在实际计算时，根据Re及，从图中查得λ值，而不必先确定属于哪一区域。

柯列布鲁克公式是隐式公式，需用迭代法求解，比较复杂。因此，人们努力寻求较为简便的显式计算公式，基本思路是依照柯列布鲁克的方法。即当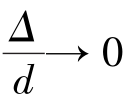时，应该变为光滑管公式，而在Re→∞时，则应当变为适用于粗糙管公式。按照柯列布鲁克方法，将式（6．58）改写为

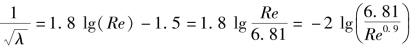
再利用式（6．51），将其合并得

此即为苏联富兰凯尔（H·З·peнкепъ）公式。同样的方法，如果将式（6．51）改写为

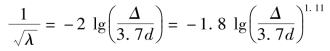
与式（6．58）合并，得

这就是我国石油工业部门常用苏联依萨也夫（H·A·Исаев）公式。可见，式（6．59）与式（6．60）尽管在结构上不同，其结果十分近似，纯属异曲同工。

1976年斯韦密（P．D．Swamee）和齐恩（A．K．Jain）提出与式（6．60）基本一样的公式，即

该式的适用范围为

在适用范围内与柯列布鲁克公式（6．59）相差在1%的范围内。除上述对数形式的公式外，还有一个指数形式的公式，即

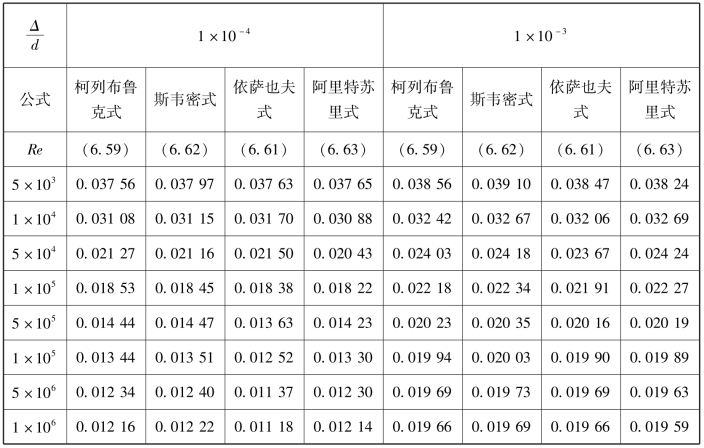
这是苏联阿里特苏里（Aпътщупъ）提出。它的推导与上述方法基本相同，都具有：当时，变为光滑管公式，而当（即Re→∞时），变为粗糙管公式（见式（6．64））。因而从式（6．60）到式（6．63）的任何一公式都可作为柯列布鲁克公式的近似。因为它们都是显式公式，用函数计算器求解都十分方便。表6．5列出了上述几个公式与柯列布鲁克公式的比较。可以看出，它们与柯列布鲁克公式的误差在1%左右。

表6．5　过渡区之λ计算公式比较

（3）粗糙管紊流区

粗糙管紊流区仍可用式（6．51），即

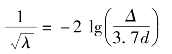
苏联希夫林松（шuфрuнсон）给出指数形式的公式，即

但是，式（6．51）被认为是最可接受的公式。

（4）胶管沿程摩阻系数

对于输油用的橡胶软管，其沿程摩阻系数可以参考以下的公式。

①螺旋钢丝胶管（紊流）

式中 λ——与胶管同直径的钢管沿程摩阻系数；

e——螺旋钢丝凸出胶管壁面的高度；

d——胶管内径；

s——钢丝圈间距。

由于螺旋钢丝胶管凸出高度e和钢丝圈间距难以确定，同时，在使用胶管的场合中，胶管的长度通常不很长，其λ值（紊流）可大致选用表6．6中的数据。

表6．6　螺旋胶管的λ值(www.daowen.com)

②平滑橡胶软管

紊流时，λ的计算公式为

λ＝0．01113＋0．917Re－0．41　（6．66）

式（6．65）及式（6．66）是直胶管的计算公式。按该式算得的λ值视胶管安放情况可适当增大10%左右。

对于其他类型的软管可采用下列近似的λ值：

a．普通的麻织软管：λ＝0．0418

b．好的革制软管：λ＝0．0270

例6．5 输送石油的管道长l＝5000m，直径d＝250mm的旧无缝钢管，通过的质量流量M＝105kg／h，在冬季运动黏度ν1＝1．09×10－4m2／s，在夏季ν2＝0．36×10－4m2／s，若取密度ρ＝885kg／m3，试求沿程摩阻损失各为多少？

解 ①判别流态

冬季：

夏季：

紊流时，还必须判别阻力区域。对旧无缝钢管，由表6．4，取Δ＝0．18mm，则据式（6．53）得

故流动处于光滑管紊流。

②计算沿程摩阻系数

夏季：因Re2＜105，且处于光滑管紊流，用伯拉修斯公式（6．57）得

③求沿程摩阻损失

冬季：

式中，

夏季：

例6．6 已知铸铁输水管长l＝500m，直径d＝150mm，输水流量Q＝160m3／h，若水温为20℃（ν＝0．0131St），求沿程摩阻系数λ。

解 ①求雷诺数

②判别阻力区域

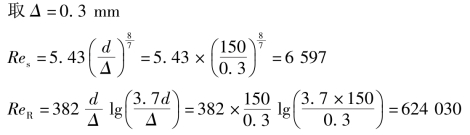
因为Res＜Re＜ReR，故流动处于紊流过渡区。

③计算

a．用莫迪图

因为

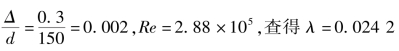
b．用式（6．62）计算

c．用式（6．61）计算

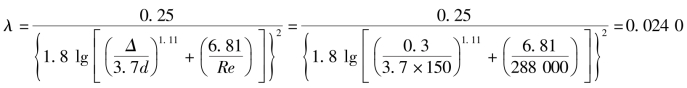
d．用式（6．63）计算

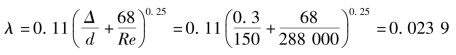
由上述各式计算结果表明，它们之间的误差都不超过1%。

例6．7 有一输油管，直径d＝150mm，内壁粗糙度Δ＝0．15mm，油的运动黏度ν＝0．05cm2／s。求流态为光滑紊流区时的最大流量和在粗糙管紊流区（阻力平方区）时的最小流量各为若干？

解 ①求光滑区时的最大流量

按式（6．53）光滑区时最大的雷诺数，即

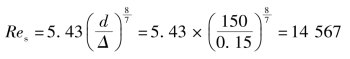
因故得

②求阻力平方区最小流量

由式（6．54）得进入阻力平方区的最小雷诺数

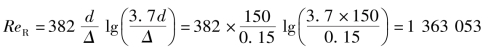
得

对于直径为150mm的输油管，不可能用这么大的流量输送（通常为左右）。由此可见，轻质油品的输油管中，流态处于平方阻力区是极少见的。