在试验方面最值得注意的是尼古拉兹的结果。尼古拉兹用人工方法制造不同粗糙度的圆管，即用漆胶将颗粒大小相同的砂粒均匀地粘贴在管壁上，砂粒直径表示管壁粗糙突出高度Δ。它用3种不同管径（25mm、50mm、100mm）和6种不同的相对光滑度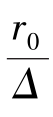值（15、30．6、60、126、252、507）进行试验，试验装置原理如图6．15所示。试验时，测定每种管道的不同的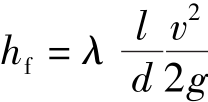流量和相应于长度为l管段的沿程摩阻损失hf，然后再根据达西公式和雷诺数公式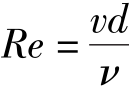计算出λ和Re，并以相对粗糙度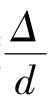为参变数，将实验结果的关系曲线绘于同一坐标纸上，如图6．16所示。

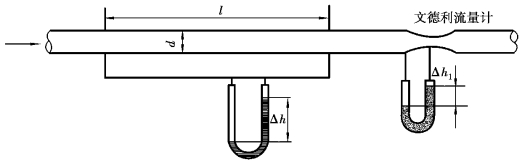
图6．15　测定管道沿程损失的实验装置

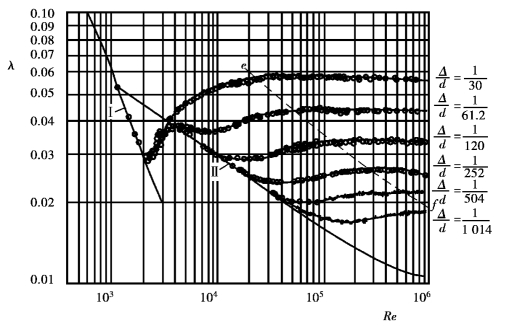
图6．16　尼古拉兹人工粗糙管沿程摩阻系数图

分析这张图，可将此曲线分成5个区域：

（1）层流区

此区即为图中的直线Ⅰ部分。当Re≤2300时，所有的6种相对粗糙度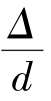的实验点都落在这条直线上，这说明层流流动时，沿程摩阻系数λ与管壁相对粗糙度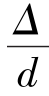无关，而只与雷诺数有关，该直线的方程为

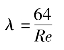
这与6．4节中理论分析得到的式（6．25）一样，证明理论分析的成果的正确性。

（2）层流到紊流过渡区

此区位于2300＜Re＜4000。不同的相对粗糙度的实验点在Re＝2300附近开始离开Ⅰ线。实验点也集中在一条很短的曲线上，但实验点稍为分散。这个区域实际上就是由层流向紊流（或相反）的转变过程。该区范围很小，实用意义不大，其计算方法略。

（3）光滑管紊流区

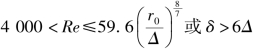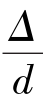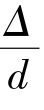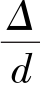此区为直线Ⅱ部分。当时，属于光滑管紊流区。各种不同的的实验点也都落在这条线上，只是不同的值，离开此线时的雷诺数Re值不同。这是由于黏性底层厚度还较大（δ＞6Δ），掩盖了粗糙突出高度Δ的影响，这就是光滑管紊流区。但是不同的，所占该直线的线段长度不同，越大，所占的线段越短，表明相对粗糙度越大，离开该线时雷诺数越小。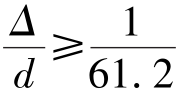的曲线，实际上没有光滑管紊流区。将实验曲线离开光滑管区时的雷诺数以Re表示，对于人工粗糙管道，有

式中，d为管道内直径。

根据式（6．18），即

式中，平均流速v可由光滑管紊流速度公式（6．45）积分求得，代入上式，简化后得

这就是光滑管紊流的普朗特阻力系数公式。它适应范围达到Re＜3×106以内。

（4）紊流过渡区

此区为线Ⅱ和ef之间，称为紊流过渡区，简称过渡区。当时，属于紊流过渡区。当雷诺数继续增大，黏性底层的厚度逐渐变薄。由图可知较大的管子，实验点在Re较小时先离开直线Ⅱ而进入该区。其他较小的管子，在Re较大时才离开。在该区内，。情况复杂，其计算公式尼古拉兹没有给出。

（5）粗糙管紊流区(www.daowen.com)

此区为ef线的右边部分。当时，为粗糙管紊流区。随着雷诺数继续增大，试验点所连成的线为一水平直线。因为在这区域内，黏性底层厚度已经变得非常薄，管壁粗糙度对流动阻力的作用已经大大超过黏滞性的影响。因此，在此区域中，沿程摩阻系数与雷诺数无关，只与相对粗糙度有关，即。卡门（Karman）依据尼古拉兹试验资料，经整理得

或

式（6．51）表明，λ与Re无关，即与v、ν无关，将其代入式（6．6），便知沿程损失与v2成正比，因此，这个区域也称为平方阻力区。另外，因为雷诺数并不影响λ值，雷诺数对流动特征、力学性能均失去影响，在此状态下的紊流如果进行模型试验，可不必考虑其雷诺数相等的条件，此时，无论原型与模型的雷诺数是否相等，只要相等，它们的黏性力都会自动保持力学相似，因此，粗糙管紊流区也称为自动模型区。

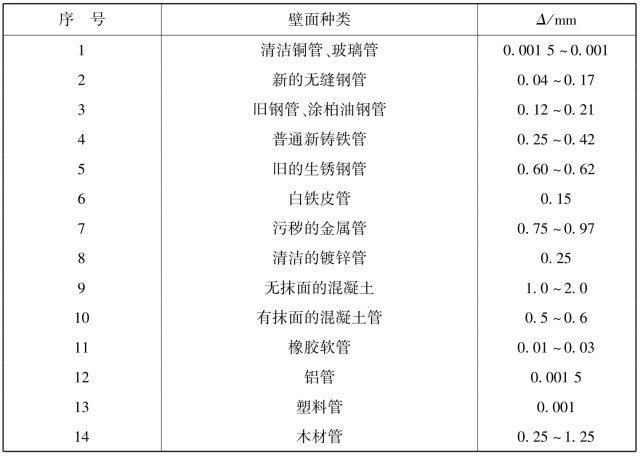
前已述及，由于天然粗糙管（即实际材料的壁面粗糙）非常复杂，迄今尚无科学的方法测定。然而尼古拉兹的实验提供了解决问题的途径，可将砂粒粗糙管的粗糙高度Δ作为工作管道壁面粗糙的量度。方法是在粗糙管紊流区内，设已知工业管道在该区内的λ值，则它的Δ值可由式（6．52）算出。因此，工业管道的Δ值称为当量粗糙度，但习惯仍称为粗糙度。各种常用材料壁面当量粗糙度见表6．4，供计算选取。

表6．4　各种材料壁面当量粗糙度Δ值

尼古拉兹的试验比较完整地反映了沿程摩阻系数的变化规律，揭示了紊流不同情况下沿程摩阻系数的影响因素。所得到的光滑管紊流及粗糙管紊流的摩阻计算公式都是依据普朗特的混合长度理论及速度分布公式的基础上得到的，它们的精确度较高。但是，工程中采用实际管道（钢管、铸管铁管、水泥管、塑料管等）的粗糙度与尼古拉兹的人工均匀粗糙度是不同的。对于实际管道，粗糙的突出高度、形状，以及分布的稠密和特性与人工粗糙是不同的。因此，人们也对实际管道进行了大量试验研究。结果表明，所获得的曲线与尼古拉兹曲线有所不同。图6．17是苏联Ф·А谢维列夫（Ф·А·Щевепев）对不同直径的新钢管（尽管Δ不完全一样，但d不同，可得不同的值）进行试验的结果。比较尼古拉兹曲线图（图6．16）和图6．17看出，对于钢管，在过渡区，系数λ的数值永远大于阻力平方区的数值，并且随雷诺数增大而不断减小；尼古拉兹所得的曲线却相反，在过渡区，λ值随雷诺数的增大而增大，最后达到最大值，过渡区的λ值永远小于阻力平方区的数值。其次，还可以看出：在相同相对粗糙度的条件下，实际管道的雷诺数从光滑管区进入过渡区时要比人工粗糙管小得多，主要原因是实际管道的壁面粗糙尺寸大小不均匀，分布特性不规则，虽然雷诺数较小，即使黏性底层较厚的时候，尺寸较大的粗糙凸起高度首先对流动阻力发生了影响，因而在较小的雷诺数时就进入过渡区。根据对试验资料整理，对于钢管，流动由光滑管区进入过渡区时约略地在

发生，即时，流动处于光滑管紊流区。

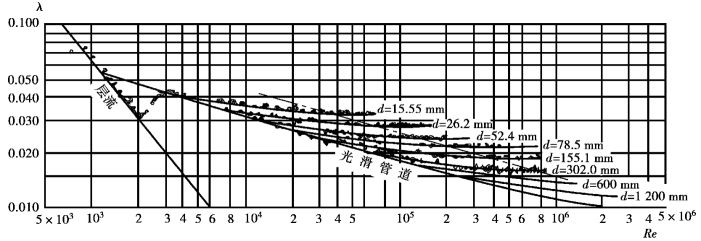
图6．17　新钢管的λ＝f（Re）图

至于由紊流过渡区到达阻力平方区的雷诺数ReR，也比人工粗糙管要小些，但相差不很大。用ReR表示由过渡区进入阻力平方区时的雷诺数，则根据资料整理，可用下式计算，即

也可用下式近似计算，即

综上所述，工业管道紊流3个阻力区的分界准则为：

①光滑管紊流区：

②紊流过渡区：

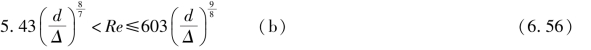
③粗糙管紊流区：