本节介绍由混合长度理论导出的流速分布。混合长度理论的重要贡献之一，就在于它能够用来导出高雷诺数下的流速分布。

在黏性底层中，其切应力为（注意：此后各参数均省略去时均值符号）

因为黏性底层很薄，速度梯度近似为常数，所以层内的切应力τ＝常数，它就是壁面上的切应力τ0，于是积分得

由此可知，在黏性底层中速度分布是直线规律，这显然是层流速度抛物面规律在黏性底层中的近似结果。

，它具有速度量纲，称为剪切速度，则式（6．41）可写为

在紊流区，即黏性底层外，y＞δ，黏性影响可以忽略，则式（6．39）成为

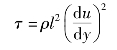
普朗特假设在靠近壁面处混合长度l与y成正比例变化（因为y越大，质点的紊动自由越大，紊流切应力也应越大），即l＝ky。根据尼古拉兹（J．Nikuradse）的实验资料证明，这个规律可以扩大到整个紊流区域。此外，还假设在整个紊流区内剪应力也为常数τ0，则：

或

积分之得

这说明紊流区中速度u与y成对数关系。积分常数C由边界条件确定，也可根据管道轴心处的最大速度umax来确定。例如，对光滑管紊流，设紊流区与黏性底层交界面上的速度为uw，由式（6．42），当y＝δ时，有

式中，N是根据上式推理，即由黏性底层转变成紊流时，应有一个临界值，因为形式上是一个雷诺数；另一方面，当y＝δ时，u＝uw代入式（6．43），并利用式（6．44）得

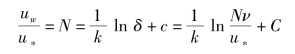
消去常数C得

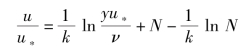
令

得

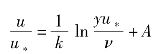
式中，A可通过实验绘制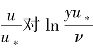的曲线而求得。对于平板，k＝0．417，A＝5．84，而对于光滑管，尼古拉兹实验得k＝0．4，A＝5．5。代入上式，得光滑管紊流速度分布公式，即

(www.daowen.com)

或

在圆管轴心上，y＝r0，u＝umax，代入式（6．45）及式（6．45a）后并与该式相减得

式（6．46）及式（6．46a）称为普朗特公式。由于消去了常数5．5，并经大量实验证明，此式对光滑和粗糙管都适用。

对于圆管紊流，普朗特推导了一个使用较方便的指数速度分布公式，即

式中，n随雷诺数而变。这个经验公式仅适用于离开管壁一定的距离。表6．3列出了Re与n的数值。

表6．3　Re与n的数值

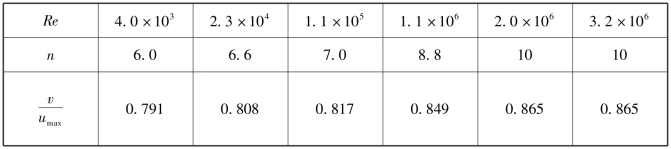
由式（6．47），可求得断面平均流速与最大流速的比值，即

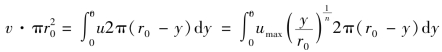
得

表6．3中也列出了对应于n的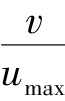值，因而可通过测定紊流管轴处最大流速umax，利用表6．3内的比值换算得平均流速v，即可算出流量，十分简便。

流速分布公式（6．45）及式（6．47）都存在着在管轴处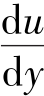为非零值的缺陷，这与实际应为零是相矛盾的。尽管如此，它们与实际相当逼近，用这些方程来描述光滑管紊流还是极其有用的。

求流速分布公式的主要目的是要由此导出沿程摩阻系数λ的公式，由于其推演过程比较繁杂，且伴有实验数据修正，本书限于篇幅，这里不再详细叙述，读者如有兴趣，可参阅其他有关的流体力学文献。

例6．4 求管道紊流平均流速v与最大流速umax之间的关系。

解　由式（6．46）得

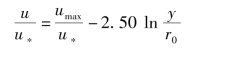
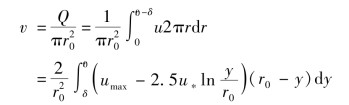
因为紊流公式仅适用于紊流区，故不能积分到y＝0。但层流底层区的流量是如此之小，以致可以不计，于是

积分得

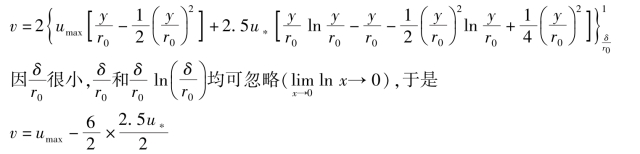
即