（1）紊流阻力

在紊流中，一方面因时均流速不同，各流层间的相对运动，仍然存在着黏性切应力，另一方面还存在着由脉动引起的动量交换产生的惯性切应力。因此，紊流阻力包括黏性切应力和惯性切应力。

黏性切应力可由牛顿内摩擦定律计算。下面首先分析惯性切应力的产生原因。

在图6．12所示的恒定紊流中，时均流速沿x轴方向。脉动流速沿x和y方向的分量分别为u′x和u′y。任取一水平截面A—A，设在某一瞬时，原来位于低流速层a点处的质点，以脉动流速u′y向上流动，穿过A—A截面到达a′点，则单位时间内通过A—A截面单位面积的流体质量为ρu′y。由于流体具有x方向的流速，其瞬间时值为ux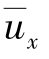＝＋u′x，因而也就有x方向的动量由下层传入上层。单位时间内通过单位面积的动量为ρu′y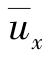（＋u′x），这样，截面A—A的下侧流体损失了动量，而上侧的流体增加了动量。根据动量定律：动量的变化率等于作用力。这里动量的变化率也就是通过截面A—A的动量流量。因此，由横向脉动产生的x方向的动量传递，使A—A截面上产生了x方向的作用力。这个单位面积上的切向作用力就称为惯性切应力。用τ2表示，即

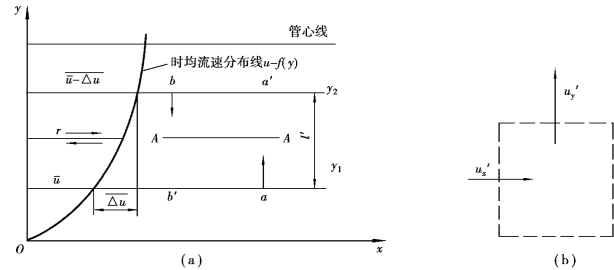
图6．12　紊流的动量交换

这里u′x和u′y可能为正，也可能为负。图中所示流动的黏性切应力用τ1表示。τ2的时均值，根据式（6．28），有

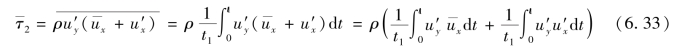
上式中，平均值ux与积分变量无关，不难证明脉动量的时均值为零。

因为uy＝uy＋u′y，两边取时均值，得

所以

于是

现在分析惯性切应力的方向。当流体由下往上脉动时，u′y为正，由于a点处x方向的时均流速小于a′处的时均流速，因此，当a处的质点到达a′处时，在大多数情况下，对该处原有的质点的运动起阻滞作用，产生负的沿x方向的脉动流速u′x；反之，原处于高流速层b点的流体，以脉动流速u′y向下运动，则u′y为负，到达b′点时，对该处原有的质点的运动起向前推动的作用，产生正值的脉动流速u′x。这样正的u′x和负的u′y相对应，负的u′x和正的u′y相对应，其乘积u′xu′y总是负值。此外，惯性切应力和黏性切应力的方向是一致的，下层流体（低流速层）对上层流体（高流速层）的运动起阻滞作用，而上层流体对下层流体的运动起推动作用。

为了使惯性切应力的符号与黏性切应力一致，以正值出现，因此，在式（6．34）中加一负号，得

上式就是流速横向脉动产生得紊流惯性切应力，是雷诺于1895年首先提出的，故又称雷诺应力。但要提醒的是，即使对平均流动而言，流动朝着同一方向的紊流（例如直管内流动）在三个坐标方向都存在着流速的脉动分量。因此，一般的惯性切应力还在其他方向上存在。

时均紊流总的切应力为τ＝τ1＋τ2，紊流切应力分为布如图6．13所示。

由于脉动量测量困难，因此利用脉动量直接计算惯性切应力实际上是不可能的。由于脉动量的存在和应用上主要关注的是平均值，因此，紊流理论主要就是研究脉动值和平均值之间的相互关系。紊流研究的方向主要有：

①紊流的统计理论；

②平均量的半经验理论。

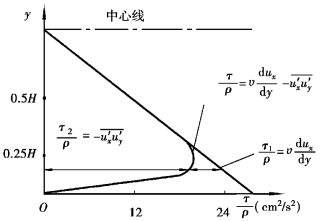
图6．13　紊流切应力分布

半经验理论是工程中主要采用的方法。1925年普朗特提出的混合长度理论，就是经典的半经验理论。(www.daowen.com)

（2）混合长度理论

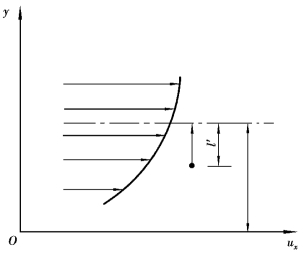
图6．14　普朗特混合长度

宏观上流体微团的脉动引起惯性切应力，这与分子微观运动引起黏性切应力十分相似。因此，普朗特假设在脉动过程中，存在着一个与分子平均自由路程相当的距离l′，如图6．14所示。微团在该距离内不会和其他微团相碰，因而保持原有的物理属性。例如，保持动量不变，只是在经过这段距离后，才与周围流体相混合，并取得与新位置上原有流体相同的动量等。

现根据l′的两层流体的时均流速差为

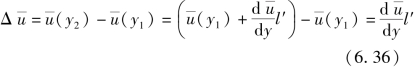
由于两层流体的时均流速不同，因此横向脉动动量的结果要引起纵向脉动。普朗特假设纵向脉动流速绝对值的时均值与时均流速差成比例，即

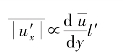
同时，在紊流里，用一封闭边界隔离出一块流体，如图6．12所示。普朗特根据连续性原理认为：要维持质量守恒，纵向脉动必将影响横向脉动，即u′x与u′y是相关的。因此，与成比例，即

虽然与不等，但可以认为两者成比例关系，符号相反，则

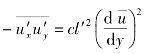
式中，c为比例系数，令l2＝cl′2，则上式可变为

这就是由普朗特的混合长度理论得到的以时均流速表示的紊流惯性切应力表达式，式中l称为混合长度。于是，紊流切应力可写为

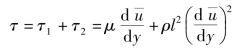
层流时只有黏性切应力τ1，紊流时τ2有很大影响，如果将τ1和τ2相比，则

是雷诺数的形式，因此，τ2和τ1的比例与雷诺数有关。雷诺数越大，紊动越剧烈，τ1的影响就越小，当雷诺数很大时，τ1就可以忽略了，于是

为了简便起见，从这里开始，时均值就不再标以时均符号。

在式（6．39）中，混合长度l是未知的，要根据具体问题作出新的假定，结合实验结果才能确定。普朗特关于混合长度的假设有其局限性，但在一些紊流流动中应用普朗特半经验理论所获得的结果与实践比较一致。

将式（6．39）运用于圆管紊流，可以从理论上证明断面流速分布是对数型的，即

式中，y为离圆管壁的距离；k为卡门通用常数，由实验定；C为积分常数。

层流和紊流时，圆管内流速分布规律的差异是由于紊流时流体质点相互掺混使流体分布趋向于平均化造成的。层流时的切应力是由于分子运动的动量交换引起的黏性切应力；而紊流切应力除了黏性切应力外，还包括流体微团脉动引起的动量交换所产生的惯性切应力。由于脉动交换远大于分子交换，因此在紊流充分发展的流域内，惯性切应力远大于黏性切应力，也就是说，紊流切应力主要是惯性切应力。