如果在雷诺实验的玻璃管B上取1⁃1及2⁃2断面，并在这两个断面上装测压管，如图6．5所示。对该两断面列总流伯努利方程为

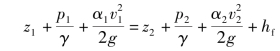
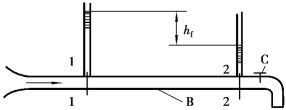
图6．5　水头损失与流速的关系

因为试验管是等直径的，所以

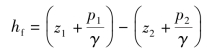
即两根测压管的水头差等于1⁃1、2⁃2断面间沿程损失。在层流和紊流情况下，逐次测出hf及相应的管中平均流速v，并在对数坐标纸上将试验点标出，得出如图6．6所示的曲线。曲线中ABCD表示逐渐增大流速的情况，而DCEA则表示逐渐减小流速时的情况。由图可知，层流时的试验点落在图中的AB线上，这是一条与lgv轴成45°角的斜线。紊流时试验点落在一条较大倾角θ的斜线CD段上。

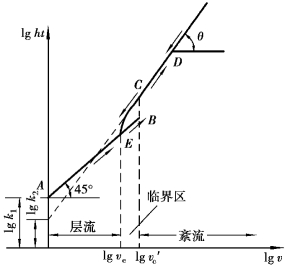
图6．6　沿程摩阻损失与平均流速的关系

如果将其写成函数式，对于层流，则

lghf＝lgk1＋（lgv）tan45°＝lgk1v

所以

hf＝k1v　（6．11）

即层流时沿程损失与速度的一次方成正比。

对于紊流，则(www.daowen.com)

lghf＝lgk2＋（lgv）·tanθ

令tanθ＝m，则

lghf＝lgk2＋mlgv＝lgk2vm

所以

hf＝k2vm　（6．12）

即紊流时沿程损失与速度v的m次方成正比。试验表明，m＝1．75－2。即hf与v的1．75～2次方成正比。

由此可见，层流及紊流不仅现象不同，而且对沿程损失的影响规律也不同，因此，在计算沿程损失时，应当将它们区别开来。

例6．1 直径为100mm的输油管，以流量Q＝50m3／h输送喷气燃料，已知其运动黏度ν＝1．2cSt，试确定流动形态。

解 管道中的平均流速为

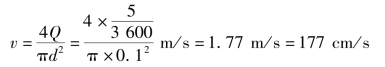
而ν＝1．2cSt＝0．012cm2／s

所以

因雷诺数147500大于下临界雷诺数2300，所以是紊流。