虽然层流和紊流早已被人们所知，但是直至1883年才由雷诺（OsborneReynolds，英国科学家）进行了定量描述，他的实验装置如图6．2所示。由水箱A引出玻璃管B，阀门C用以调节玻璃管中液体的流量。容器D内装有重度和水相近的颜色水，经细管E流入玻璃管中，阀门F用来调节颜色水的流量。试验时，容器A装满水，并使液面恒定，由K不断供水而多余的水由溢水管H溢出；然后稍微打开阀门C，便有少量的水经玻璃管流出，此时打开颜色水的阀门F，使颜色水也流入玻璃管中。

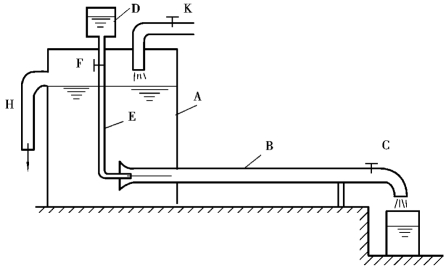
图6．2　雷诺实验

当玻璃管中流量小时，看到其中颜色呈明显的直线形状，如图6．3（a）所示，这说明整个管中的水都沿轴线方向流动，液体质点没有横向运动，不互相掺混，这种流动状态就是层流。若将阀门C继续徐徐开大，玻璃管中流速增大，当达到某一流速数值时，颜色水的线状出现微微震动（或摆动），如图6．3（b）所示。继续开大阀门C，流速相继增大，颜色水不再保持线状，而破裂成一种非常紊乱状态，如图6．3（c）所示，说明此时玻璃管中水的质点互相混掺，这种流动就是紊流。紊流时，液体质点的运动轨迹是极不规则的，不仅沿管轴方向有位移，而且也有沿管径方向的位移。固定点上的速度大小和方向是随时间而变的。

如果试验程序沿相反方向进行，即在紊流情况下将阀门C徐徐关小，则颜色水将回到图（b）的形状，再关小又回到图（a）的形状。将图（b）的那种运动状态称为临界状态或过渡状态，而临界状态时的平均速度称为临界流速。

试验表明：

①如果管径一定，液体的黏度ν一定，则由层流转变为紊流时的临界流速v′c（称为上临界流速）和由紊流变成层流时的临界流速vc（称为下临界流速）是不一样的，v′c＞vc。

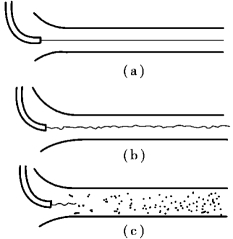
图6．3　层流、临界状态及紊流

②临界流速的数值与管径d及液体的黏度ν有关。但是，无论临界流速、管径及黏度ν怎样变化，临界状态时的雷诺数（称为临界雷诺数）是不变的。相应于上临界状态时的雷诺数，以Re′c表示；相应于下临界状态时的雷诺数，称为下临界雷诺数，以Rec表示。大量试验表明：

上临界雷诺数

下临界雷诺数

上临界雷诺数是不稳定的，其数值与试验装置的状况及试验时所受到的扰动等情况有关。有的甚至达到40000，而下临界雷诺数却是稳定的。因此，在工程计算中，以下临界雷诺数作为判别流动形态的标准，即

(www.daowen.com)

准则式（6．9）是管道中流动形态的判别准则。欲知管道中的流动形态，只要算出管道流动时的雷诺数Re和Rec比较，便可知流动是层流或紊流。

对于非圆断面的管道，因为雷诺数的一般表达式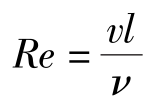中的特征长度尺寸l在圆形管道中为直径d，但在非圆形断面管道中用什么作为特征尺寸呢？下面的关系式：

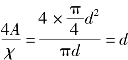
由上式得到启发，式中A是过流断面积，χ是流体与过流断面固体壁面的接触周长。因此，非圆形管道的特征尺寸可以用过流断面积与过流断面上流体与固体接触的周长比值的4倍来表示，即

式中，dH称为等效直径或水力直径，χ在水力学中称为湿周。这样，非圆断面管道的雷诺数，它与圆形管道是一致的。

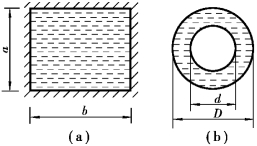
图6．4　非圆形断面

例如，如果断面是矩形如图6．4（a）所示的管道，等效直径为

如果断面是环形如图6．4（b）所示的管道等效直径为

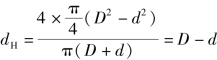
某些非圆形断面的下临界雷诺数，根据实验见表6．1。

表6．1　非圆形管道的下临界雷诺数

雷诺试验不仅显示了黏性流体存在不同的流态，而且也揭示了不同流态时摩擦阻力的性质。