量纲分析法有两种:一种方法是雷列法,它是应用量纲和谐原理建立物理方程,但它只适用于比较简单的变量不超过四个的物理过程;另一种方法是布金汉(Buckingham)的π定理。π定理是具有普遍性的方法,也是以下要介绍的方法。
π定理是这样定义的:任何一个物理过程,如果包含有n个物理量,涉及m个包含所有基本量纲的基本物理量,则这个物理过程可由n个物理量组成的(n-m)个量纲一的量π所表达的关系来描述,其中π是一个量纲一的独立参数。
例如,影响某一物理过程的n个物理量为A1,A2,A3,…,An,则这个物理过程可用一个函数表示,即
f(A1,A2,A3,…,An)=0 (5.20)
如果这些物理量含有m个基本物理量,根据π定理,这个物理过程也可用(n-m)个量纲一的组合量π表示的关系式来描述,即
F(π1,π2,π3,…,πn-m)=0 (5.21)
与式(5.20)比较,式(5.21)所包含的变量比式(5.20)减少了m个,而且是量纲一的量。这就使得式(5.21)具有重要的优点,这些优点通过以后的例题可以看出。
π定理可以从数学上得到证明,此处从略。以下首先说明π定理应用的步骤,然后举例。
应用步骤如下:
①确定对所研究的物理过程有影响的物理量,设共有n个:A1,A2,A3,…,An,按式(5.20)写出一般函数表达式,即
f(A1,A2,A3,…,An)=0
做到这一点要求对该物理过程有足够的认识,正确地确定有影响的物理量。对流动来说,主要包括流体的物理特性、流动边界的几何特性和流动的运动特征等。影响因素(物理量)的确定是否全面和正确,将直接影响分析的结果。
②从这几个物理量中选取m个基本物理量,这m个基本物理量在量纲上要求是独立的。对于力学问题,一般m≤3。水力学问题中常以代表边界几何特征量(如管径)、表征运动的量(如平均流速v)以及与力或质量有关的量为这三个基本物理量。
③列出量纲一的参数π。根据π定理,构成(n-m)个量纲一的参数π的一般表达式为
![]()
式中,A1、A2及A3为所选的3个基本物理量;Ak为除去已选择的A1、A2及A33个基本物理量以后所余下的(n-3)个变量中的任何一个物理量;xi、yi及zi为对应于πi的待定指数。如果分开写,式(5.22)可写为
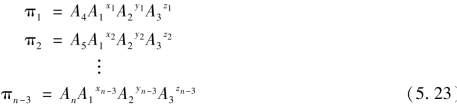
④因π是量纲一的参数,即[π]=[L0][T0][M0],所以根据量纲和谐原理,求出各π项的指数xi、yi、zi。
⑤写出描述物理过程的量纲一的关系式
F(π1,π2,…,πn-3)=0
需要指出:量纲一的参数π可以取倒数或任意次方仍不影响其为量纲一的数的性质。因此,必要时可将所得到的各π参数乘其某一次方或乘除,以尽可能使各π项成为一般熟悉的量纲一的数,如雷诺数Re、佛汝德数Fr等形式。
例5.4 求节流式流量计(如孔板、喷嘴、文德利管)的流量关系式。影响喉道(缩小断面处)流速v2的因素有:进口断面直径d1、喉道直径d2、液体的密度ρ、动力黏度μ及两个断面的压强差Δp(假定流量计水平安装)。
解 现用π定理求出这个关系式:
①根据上述确定的影响因素,n=6,可写为一般的函数关系式,即
f(v2,d1,d2,ρ,μ,Δp)=0
②从上列6个物理量中选取3个独立的基本物理量:d2、v2、ρ。
③列出量纲一的参数π,共n-3=(6-3)个=3个。

④根据量纲和谐原理,求出各π项的指数如下:
式(a):[L0T0M0]=[L][L]x1[LT-1]y1[ML-3]z1
对L:0=1+x1+y1-3z1
T:0=-y1
M:0=z1
得 x1=-1,y1=0,z1=0
由此得
![]()
同理求得
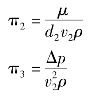
⑤将各π项代入式(5.21)得
![]()
即
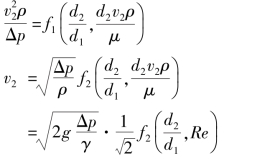 (www.daowen.com)
(www.daowen.com)
由此得节流式流量计流量一般计算公式,即
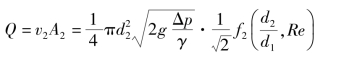
式中,量纲一的函数![]() 实际是一个系数,可由试验或分析进一步确定。可以看出,应用量纲分析法后,便找到了表达所研究的物理过程的一个具体关系式,这个关系式将原来6个变量关系简化为3个量纲一的参数之间的关系,即
实际是一个系数,可由试验或分析进一步确定。可以看出,应用量纲分析法后,便找到了表达所研究的物理过程的一个具体关系式,这个关系式将原来6个变量关系简化为3个量纲一的参数之间的关系,即
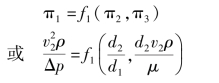
如果这个函数关系式![]() 只能由试验确定,则试验次数将大大减少。例如,要测取几种不同比值
只能由试验确定,则试验次数将大大减少。例如,要测取几种不同比值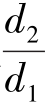 的孔板流量计之函数
的孔板流量计之函数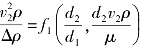 ,只需将每种
,只需将每种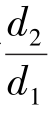 作为固定参数,然后测取不同的
作为固定参数,然后测取不同的![]() 值,绘制成如图5.2所示的关系曲线。这样得到的曲线十分清晰,使用也很方便。更重要的是试验非常方便,因为此时不需要用不同密度ρ和不同黏度μ的液体,要使量纲一的量
值,绘制成如图5.2所示的关系曲线。这样得到的曲线十分清晰,使用也很方便。更重要的是试验非常方便,因为此时不需要用不同密度ρ和不同黏度μ的液体,要使量纲一的量![]() 变化,可以在保持ρ、μ及d不变的情况下,仅改变速度v即可。22
变化,可以在保持ρ、μ及d不变的情况下,仅改变速度v即可。22
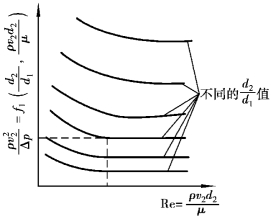
图5.2 量纲一的函数关系曲线
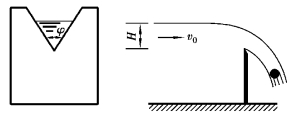
图5.3 薄壁三角堰
例5.5 已知通过薄壁三角堰的液体流量Q与下列因素有关:堰上水头H(图5.3)、重力加速度g,行近流速v0及堰口角φ,求该种堰的流量关系式。
解 此处共有5个物理量:
①写出一般函数式,即
f(Q,H,g,v0,φ)=0
②这5个物理量中所涉及的基本量纲只有[L]及[T]两个,所以,m=2,选取H及g为基本物理量。
③求量纲一的π,即
π1=Hx1gy1Q
π2=Hx2gy2v0
π3=φ
④求出各量纲一的量π的指数x及y
求π1:π1=Hx1gy1Q=[L]x1[LT-2]y1[L3T-1]=[L0T0]
对L x1+y1+3=0
对T -2y1-1=0
解得![]()
故![]()
求π2:π2=Hx2gy2v0=[L]x2[LT-2]y2[LT-1]=[L0T0]
对L x2+y2+1=0
对T -2y2-1=0
解得![]()
故![]()
于是,其一般关系式为
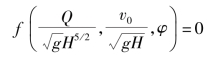
或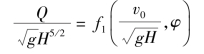
解得Q
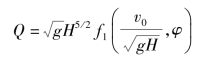
上两式中f及f1为未知函数,由试验或分析确定。如果选H和v0作为基本物理量代替H和g,则有
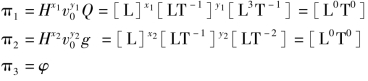
所以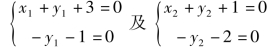
解得 x1=-2,y1=-1及x2=1,y2=-2
故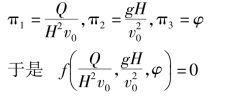
因为π参数可以取其倒数或乘任意次方而不影响其量纲一的状况,所以上式可写为
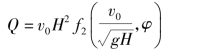
未知函数f2具有与f1相同的参数,但它们却不是相同的函数。后面这个公式不是非常有用,因为一般情况下对三角堰行近流速v0可以忽略,这表明较次要的物理量不宜选作基本量。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






