根据不可压缩黏性流体的运动方程(N⁃S方程)在直角坐标系x轴的分量表示式,即
式中,ν为流体运动黏性系数。此式对于两个力学相似的流场均适用,所以对原型流场可写为:
同理,对模型流场可写为
由几何相似,各相应线段成比例,即
由运动相似,各相应点的速度成比例,即
由动力相似,各相应点的压强及质量力分别成比例,即
式中,G为作用在单位质量液体的质量力,X、Y、Z分别为G在三个坐标轴上的投影。同时,假定两个流场相应点处的密度和黏性系数成比例,即
将式(a)到式(d)各式改为“原型量=比尺×模型量”的形式,即
代入式(5.8)整理得
比较式(5.9)和式(5.10)知,式(5.10)的各项为式(5.9)各对应项乘上一个由比尺组成的系数。而两式中的各对应项代表作用于两个力学相似流动中相应质点上的同名力。将式(5.10)的各项分别除以式(5.9)的各对应项,可得原型和模型相应质点上的各同名力之比为
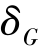 ——作用于单位质量流体质点上的质量力之比。
——作用于单位质量流体质点上的质量力之比。
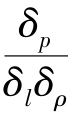 ——作用于单位质量流体质点上的压强差之比。
——作用于单位质量流体质点上的压强差之比。
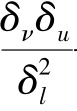 ——作用于单位质量流体质点上的黏性力之比。
——作用于单位质量流体质点上的黏性力之比。
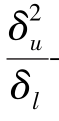 ——作用于单位质量流体质点上的变位(位移)惯性力之比。
——作用于单位质量流体质点上的变位(位移)惯性力之比。
根据动力相似的条件,上述比值应相等,即
上式表明,若两个流动系统是力学相似的,则式(5.10)中各项由比尺组成的系数相等。将式(5.11)除以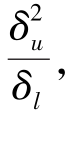 得
得
即
将各比尺还原为原型量与模型量之比,代入式(5.13),然后将原型与模型的量分别写于等号两边,则得
式(5.14)中的四个等式,若不考虑原型及模型的脚注,每个等式的两边形式完全相同,而且它们都是纯数,常用下列符号和名称表示,它们的物理意义附后。
![]() ,佛汝德数=惯性力/重力
,佛汝德数=惯性力/重力
![]() ,雷诺数=惯性力/黏性力
,雷诺数=惯性力/黏性力
![]() ,欧拉数=压力/惯性力
,欧拉数=压力/惯性力
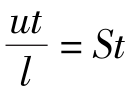 ,斯特罗哈数=定位惯性力/变位惯性力
,斯特罗哈数=定位惯性力/变位惯性力
在实际计算时这几个数中包含的长度l常取能够代表该流动几何特性的某一长度,如水深h、管径d等,l称为特征长度。这样,式(5.14)可简写为
FrP=FrM,ReP=ReM,EuP=EuM,StP=StM
若原型和模型两个流动系统是力学相似的,则它们相应点处的佛汝德数、雷诺数、欧拉数和斯特罗哈数应分别相等;反之,若原型和模型两个流动相应点处的上述四个数分别相等,则这两个流动是力学相似的。于是,这四个数即可作为判别两个不可压缩黏性流体系统是否力学相似的准绳,称为相似判据或相似准则。
以上结论是由x方向的纳维—斯托克斯方程导出的,同理,对于y、z两个方向的纳维—斯托克斯方程,可得完全一样的结果。此外,另一微分方程,即连续方程不能提供新的判据。
综上所述,两个流动系统力学相似的充分必要条件是:同时满足相应点处的上述四个数分别相等。如果从作用于流体质点上的合力的角度,而不是从各个不同物理性质的分力的角度来讨论力学相似,也可以将这四个数用一个数——牛顿数来代替。
对于两个相似流动的相应质点,质量分别为mP及mM,体积分别为VP及VM,密度分别为ρP及ρM,加速度分别为aP及aM,合力各为FP及FM。由牛顿定律知FP=mPaP=ρPVPaP及FM=mMaM=ρMVMaM,则力的比尺为
即
所以
不考虑脚标,记![]() ,为一纯数,称为牛顿数。式(5.17)可写为
,为一纯数,称为牛顿数。式(5.17)可写为
NeP=NeM (5.18)
即如果两个流动是力学相似的,它们相应点处的牛顿数应相等;反之,相应点处的牛顿数相等,则两个流动必是力学相似的。对其他流动还可以推出另外一些相似准则,如马赫相似准则和张力相似准则等。
若两个流动所有点均满足N⁃S方程,则只需要在流场中任取一对应点或相应截面满足上述相似判据即可,即任一点满足,其他所有点也必然满足。
通常针对具体问题,用两个流动的“特征”量来表示上述判据的数值,如用管径D作特征长度。(www.daowen.com)
相似判据中的任一物理量用其差值代替时所得新的判据仍然是相似判据,例如,欧拉判据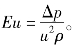
实际中的许多流体力学问题要保证完全的动力相似,即几个数据都相等是非常困难的。现举同时满足Re数相同及Fr数相同的情况为例。
对于大多数实际问题,质量力只有重力,并且重力加速度g在地面各处的变化极小,可以取gP=gM=g。因此,对于两个流动写出下式,即
由雷诺判据,ReP=ReM,即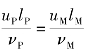
可得
由佛汝德判据,FrP=FrM,即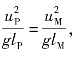 可得
可得
要同时满足Re数和Fr数为常数的条件,就要使得以上分别按照两个数各为常数所导出的模型流速uM值相等,即
或
通常δl>1,这就要求νM<νP。也就是说,模型中必须选择黏性很小的流体进行试验。例如,当δl为20及50时,如果原型中使用的流体是水,那么模型中使用的流体的黏性将是水的黏性的1/90及1/354,这种黏性的流体在自然界是不存在的,而人工制造显然也不实际。因此,在一般情况下同时满足两个判据,即同时实现两种作用力的相似,技术上是很困难甚至是不可能的,更不用说同时满足更多个力的相似了。
在特定条件下,流动可以同时满足摩阻力相似和重力相似。若两个流动处于阻力平方区(又称自动模拟区),即使相应的两个雷诺数不相等,它们的摩阻力也是自动相似的。
在有多种力作用的情况下,只能根据对现象的物理性质的分析,找出其起主要作用的力,满足这个主要力的作用,而忽略其他次要力的相似。例如,对于恒定流动,斯特罗哈数可不考虑,因为在方程中定位加速度这一项等于零;若体积力(重力)可以忽略,则佛汝德数可不考虑;如黏性力很小可以忽略,则雷诺数判据可不考虑;若压强不随坐标而变化或变化很小,则欧拉数可不考虑。
在确定根据什么判据来使流动力学相似时,必须首先对流动的受力情况作必要的分析,对大多数流动现象,主要是Re数或Fr数作为判据;在有压管道中,以Re数判据为主;在明渠、堰流及消能等问题中,则以Fr数为主;在水轮机中,要求满足St数和Eu数相等,而忽略重力相似和黏性力相似,此时,St数和Eu数则采用与水轮机特性有关的数值来表示。
例5.1 有一直径为15cm的输油管,管长5m,管中要通过流量为0.18m3/s,现用水作模型试验,管径为5cm,水温10℃,原型的油的运动黏度vP=0.131cm2/s,问水的模型流量应为多少才能达到相似?若测得模型lM相应管段上的压强水头差为3cm,试求输油管每千米的压强差是多少(用油柱表示)?
解 ①因管中流动主要受黏性摩擦力作用,所以根据相似条件应满足雷诺准则,即
Rep=ReM
即![]()
化简得![]()
由此得
将已知的dP、dM、νP及水10℃时νM=0.0131cm2/s代入上式得
②研究压强差问题,须欧拉准数相等,即
因为![]()
一般情况下,gM=gP,故得原型5m长的用油柱表示的压差为
则输油管每千米压强水头差为
例5.2 一个潜水艇以5m/s的速度在0℃的海里行驶,①求比例尺为20的模型在淡水(20℃)中行驶速度vM;②如果模型的推力是200kN,那么潜水艇本身所需的功率是多少?
解 海水在0℃时,ρP=1028kg/m3
μP=18.86×10-4Pa·s
淡水在20℃时,ρM=998.3kg/m3
μM=10.02×10-4Pa·s
①计算模型速度
因为潜艇在水下行驶受到的作用力主要为黏性摩擦力,所以
②计算原型的功率
按牛顿准则得
故得原型功率P功率=∑FPvP=688064×5W=3440.32kW
例5.3 设计一台离心式输油泵,其转速为n=1450r/min,准备选用较实物小1倍的模型输送空气进行实验。已知油的运动黏度νP=0.3cm2/s,20℃空气的运动黏度νM=0.15 cm2/s,求模型泵的转速为多少?
解 根据题意应满足雷诺数相等,即
因为![]()
所以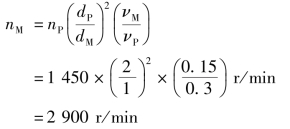
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。

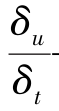 ——作用于单位质量流体质点上的
——作用于单位质量流体质点上的





