相似概念最早出现于几何学。如果两个几何图形的对应夹角相等，对应边成比例，那么这两个几何图形是相似的。这一概念可被推广于一般的物理过程。

所谓两个系统是相应的，就是假定一个系统的一个点和瞬时（xp，yp，zp，tp）可以和另一系统的唯一的一个点和瞬时（XM，YM，ZM，tM）相对应，并且假定连续性条件适用于这两个系统中的任何两个相邻点。

所谓同名物理量，即两个系统中表示同一物理属性的量。例如，一个系统中某点的速度和另一系统中相应点的速度是两个系统中的同名物理量。

当两个相应系统中进行着同一的物理过程（例如都是机械运动），而所有相应点的同名物理量的方向相同，其大小之间保持着同一比例关系，那么这两个系统就是物理相似的。

在流体力学中，两个流动系统中相应点的各种向量物理量彼此之间相互平行，并且向量或标量物理量互相成一定比例，则称两个流场是力学相似的。

要实现力学相似，两个流场必须具备几个条件：①几何相似；②运动相似；③动力相似；④边界条件和起始条件相似。

（1）几何相似

如果两个流场几何形状相同，它们所有相应线段长度之比为同一常数，那么这两个流场是几何相似的。

为了区别于两个流场的同一物理量，在该物理量符号右下角标以“P”表示原型量，以“M”表示模型的量，则lP、lM分别表示原型和模型中相应的线段，δ表示比例尺，则

长度比尺

δl表示原型尺寸与模型尺寸的比例，即它们之间的倍数关系。同理

面积比尺

体积比尺

即面积比尺和体积比尺分别为长度比尺的平方和立方。

（2）运动相似

如果两个边界条件相似的流场中任一对应点同一运动学的量方向相同，大小成比例，则这两个流场是运动相似的。

若原型某点的速度uP，模型相应点的速度uM，则

速度比尺(www.daowen.com)

同理，加速度比尺

而u＝l／t，a＝l／t2

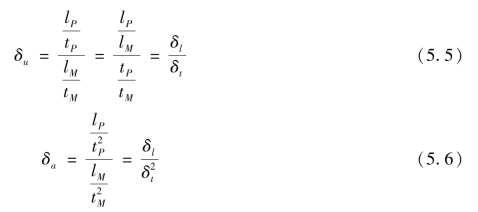
式中，δt为时间比尺。

若两个流场运动相似，其速度比尺、加速度比尺、长度比尺和时间比尺之间必然满足一定的关系；反之，当两个流场的这四个比尺之间存在上述关系，则这两个流场是运动相似的。

（3）动力相似

在相应瞬时作用于两个流场中相应点处的流体质点上的各同名力之比为一常数，则这两个流场是动力相似的。

同名力是指同一物理性质的力。例如，原型流场和模型流场中相应点都作用着黏性摩擦力、重力、压力、惯性力等。同名力之比为一常数是指任何一对相应点上作用的同一个同名力的比值都相等。即原型和模型相应点上作用的同名力构成的力的多边形是相似的，如图5．1所示，其对应边成比例，即

式中，G、T、P及∑F分别表示重力、黏性摩擦力、压力及这些力的合力；ma是根据牛顿第二运动定律∑F＝ma得到的，按照达朗伯原理，可视为惯性力。

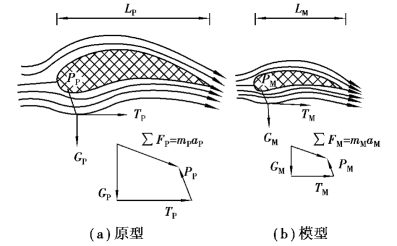
图5．1　动力相似

对于力的性质而言，除惯性力外，其余的外力（G、T、P等）的作用都是企图改变流体运动状态的，而惯性力则是企图维持流体原有的运动状态的，因此，流体运动的变化和发展就是其他物理力和惯性力相互作用的结果，各物理力之间的比例关系应以惯性力和其他各物理力的比例来表示。在两个相似的流动里，相应点的这种比例应该保持同一常数。

（4）边界条件和起始条件相似

由于一切具体的流动现象都受到与之相邻的环境影响，所以两个流动系统还要有相同性质的边界条件，才能达到力学相似。此外，任何流动过程的发展还受到起始条件的影响，即开始瞬时各物理量在流场中的分布直接影响以后的过程，对于非恒定流动过程还要求有相似的起始条件，也可从方程求解的角度来说明这一点。既然两个系统中发生着同样的物理过程，那就应该遵循同样的规律，或者说可用同样的方程来描述。因此，两个动力相似的流动应符合同样的方程。但是，当用微分方程描写物理过程时，同一类型的方程可以有很多个解，只有在一定的起始条件和边界条件下，解才是唯一的。要使两个流动的解相似，也就是使两个流动其运动及动力相似，还必须有相同或相似的边界条件和起始条件。

以上四个条件的每一个都是力学相似的必要条件，但并不充分，只有同时具备四个条件，才构成力学相似的充分必要条件。当然，这四个条件之间也不是互不相关的，例如：几何相似是运动相似的前提；仅有几何相似还不能保证它们的运动相似；若没有相似的受力情况，运动相似也是难以实现的。

从以上分析可以得出结论，如果两个流动系统是几何相似、运动相似、动力相似、边界条件和起始条件相同或相似的，则这两个流动系统是力学相似的。

要在实际工作中实现这些条件——主要指动力相似条件，就必须首先确定作用在流体上的力的性质，并给予解析地表示；其次，导出流体运动的微分方程；第三，决定流动的起始及边界条件，并给予解析表示。这就是说，为了制造模型进行试验，首先必须对作用于实际流动的力的性质及其大小有全面的了解，而这在一般情况下是不可能的。因为，如果能做到这一点，就不必要进行模型试验。而且，即便是第一、三两点都能做到的话，问题又回到了数学方面，而这一点正是要避免的。因此，问题归结为如何实现流动的力学相似条件，此外，假定力学相似条件是具备了，在模型中可以测得某处的流速或某个作用力，但根据上述力学相似条件，还不能知道原型流动的相应点的流速及同名力与模型中测得值在数量上的具体关系，还必须将相似条件化成可用以计算的关系式。