流体动力学有三大基本方程，前面已介绍了连续性方程和能量方程，现在讨论恒定总流的动量方程。在生产实践上，有些流动问题不能只用连续性方程和能量方程来解决，而要借助动量方程来解决新的问题。例如，高压消防水龙头末端的喷嘴，要解决水流喷射时对人体的冲力有多大；又如弯管中的液流，受弯管的压迫使液流转向，液流对弯管就有力的作用，这个作用力有多大；等等。应用动量方程就能很容易解决这些问题。

动量方程由动量定律推导而得。物理学上的动量定律指的是：作用在物体上的所有外力之和等于物体的动量对时间的变化率，即

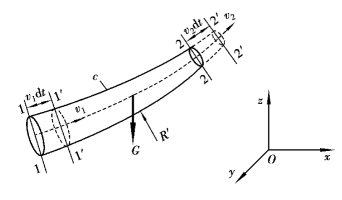
图4．15　动量方程的推导

为了将动量定律应用到流体流动中，在恒定总流内取1—1、2—2所包围的一股流体作为控制体如图4．15所示。假定该两断面都为渐变流或均匀流过流断面，在控制体的控制面内流体从断面1—1流进，从断面2—2流出。现在可以考虑流体从t时刻到t＋dt时刻内动量的变化。

在t时刻控制面1—1、2—2内的流体，在外力作用下作恒定流动，在t＋dt时刻，移动到1′—1′、2′—2′位置。由于为恒定流动，在移动过程中，1′—1′、2—2这个空间内虽有流体质点的流动和更换，但这部分流体的质量没有变，各点的流速没有变，则动量不变。因此，运动前后这股流体的动量变化等于2—2至2′—2′和1—1至1′—1′两块流体的动量差，即

由于dt很小，1—1、1′—1′和2—2、2′—2′两微段的速度、压强可认为近似不变，而

因此有

故有恒定总流的动量方程为

式中，α′为动量修正系数。对于管道层流，对于紊流，α′＝1．005～1．05。一般无特别说明，可近似取α′≈1．0。

为了便于计算，一般将动量方程写成投影形式，即

应用式（4．19）时应注意流量沿程不变，若流量沿程有变化，此时有更一般形式的动量方程，即

应用动量方程时还应注意以下几点：

①适当选取渐变流或均匀流控制断面，以便于计算断面平均流速和压强。

②作用在控制体上的外力主要包括：（a）重力G＝γV，但一般当控制体体积难以计算时，由于这部分力与其他外力比较较小，可以忽略；（b）控制体各断面上的压力，注意压强一般取表压强计算；（c）边界反力R′，注意边界反力与流体对边界的作用力大小相等方向相反，当坐标选定后，边界反力的方向可任意假设；（d）流体沿边界的摩擦阻力，通常忽略不计。

③根据题意，适当选定坐标方向，此时外力和速度对坐标轴投影时，同向为正，反向为负。

④注意动量变化为流出和流入之差，不能混淆。

⑤应用时各断面平均流速及压强计算通常还要与连续性方程和能量方程配合使用进行求解。

下面结合实例说明动量方程的应用：

例4．6 在输油管中有一段60°拐角的水平弯管，如图4．16所示。已知管道内径d＝150 mm，流量Q＝150m3／h，压强p1＝3139kPa，γ＝8500N／m3，弯管摩阻损失按计算，流动为恒定流，求油流作用在弯管上的水平力。(www.daowen.com)

解 取控制体如图4．16中的虚线所示。

由连续性方程

图4．16　输油管

由伯努利方程

得

由式（4．17）和式（4．19），并考虑恒定流，得x方向：

所以

因为假设R′x和R′y与x方向和y方向一致，所以根据作用力与反作用力的原理，流体对弯管的作用力水平分量分别为

例4．7 如图4．17所示为一喷气式飞机，其航行速度为900km／h，气体从飞机尾部喷管排出的速度为420m／s，吸入的空气量为＝26kg／s，加入燃料为吸气量的3%，求气体给飞机的推力。

图4．17　喷气式飞机

解 取如图所示虚线为控制面内的控制体，由式（4．19）得

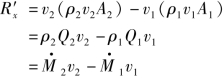
式中

代入上式

所以 R＝－R′x＝－4756N