前面已经求得实际流体沿流线或元流的伯努利方程,可以用来解决某些实际问题。但是,流线只是描述流体流动的一种抽象概念,工程实践中遇到的往往是过流断面具有有限大小的流动,即总流。因此,应将沿流线的实际流体伯努利方程推广到适用于总流上去。总流是由无数流线或元流所组成的,总流过流断面上各点,流体质点的位置高度z、压强p和流速u是不同的。利用实际流体流线伯努利方程推导总流伯努利方程时,在对总流过流断面进行积分,将遇到一定的困难,这就需要再引入一些限制条件和修正系数,使之易于用来解决工程计算问题。
(1)渐变流和急变流
在总流沿程中,流动边界可能有均匀直线的、有弯曲的、有突然扩大或缩小的、分支的等,如图4.6所示。对于流线几乎为平行直线的流动,称为渐变流。换言之,如果同时满足条件:①流线之间的夹角很小;②流线的曲率半径很大,则这样的流动称为渐变流。相反,如果不满足上述条件之一者称为急变流。渐变流是个比较含糊的概念,夹角很小,曲率半径很大,究竟多小多大,并未给予明确规定,因而在确定流动为渐变流时有一定程度的灵活性,其衡量标准就看对工程计算误差要求而定。

图4.6 渐变流和急变流
(2)渐变流过流断面的压强分布
在渐变流段上所取的过流断面称为渐变流过流断面。根据渐变流和过流断面定义,渐变流过流断面可近似认为是平面。
为了求得渐变过流断面上的压强分布,在渐变流处取断面n—n,在断面n—n取一微小柱体为隔离体,如图4.7所示。因为渐变流的流线几乎是互相平行的直线,因而作用在微小柱体的质量力只有重力(惯性力忽略)。表面力有压力和黏性阻力,但是黏性阻力是阻碍流层间作相对运动,它沿着流速方向作用,在垂直于流速方向没有分量。而微小柱体侧面上的压力与n—n垂直,对断面的压强分布也没有影响。假设微小柱体断面积为dA,柱长为dn,下底的压强为p1,上底的压强为p2,则因为垂直流速方向没有加速度分量,因此,微柱体在上述各种作用下沿断面处于平衡。沿n—n的平衡方程为
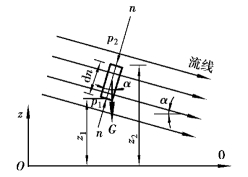
图4.7 渐变流过流断面
![]()
因为
![]()
则得

可见,渐变流过流断面上的压强按静压强分布规律分布。这个结论可用如图4.8所示的实验证实。图中是一圆直管,流动为渐变流,在同一过流断面的不同点上分别接上测压管,则测压管液面都在同一水平面上。但不同断面上有不同的测压管(水)头。对同一均匀流段而言,下游断面上的测压管(水)头要低一些,这是因为黏性阻力消耗了部分能量而使下游断面的能头降低了。
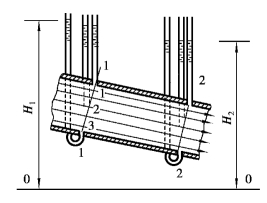
图4.8 渐变流过流断面压强分布

图4.9 急变流过流断面的压强分布
急变流过流断面上的压强分布与静压强分布规律不同。例如,液体在弯管中流动,流线显著弯曲,是典型的流速方向变化的急变流。在这种流动的断面上,有与向心加速度相反的离心惯性力的作用。与渐变流断面相比,增加了离心惯性力的作用,因此,沿离心惯性力的方向压强增加,例如,在图4.9的断面上,3个点分别接入3根测压管,则沿半径方向测压管(水)头增加。一般情况下,急变流过流断面的压强分布常常通过实测确定。
(3)恒定总流的伯努利方程
将实际流体沿流线的伯努利方程式(4.10)乘以γdQ,然后对整个总流过流断面积分,就获得恒定总流的能量关系式,即
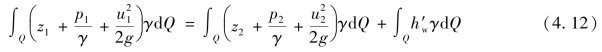
式(4.12)的各项积分,不按断面的类别,而按能量的类型,分别讨论其积分:
①势能![]() 积分
积分
这个积分表示单位时间内通过某断面A的势能总和。这个积分不易求得,但如果断面A为渐变流过流断面,则![]() 常数,则式(4.12)中势能的积分为(https://www.daowen.com)
常数,则式(4.12)中势能的积分为(https://www.daowen.com)
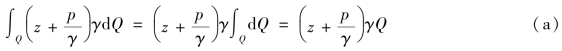
②动能![]() 的积分
的积分
此积分为单位时间内通过断面A的流体动能总和。因为断面上流速u是变量,通常其在断面上的分布规律不易求得,常用平均流速来计算。但由此必然会引起计算误差,因而用一个系数α来加以修正。此时有
![]()
由式(b)可以看出,要使得等式成立,则有

系数α是断面上的实际动能与以平均流速计算的动能的比值,称为动能修正系数。它的值总是大于1,并与流速分布有关,流速分布越不均匀,α值越大,当流速分布较均匀时,α接近于1。对于管道,当流态为层流时,α=2;当流态为紊流时,α=1.05。
③∫Qh′wγdQ的积分
这个积分与第①、第②类积分不同,它不是在断面上的。它表示单位时间内流体克服在总流两断面间的摩擦阻力做功而消耗掉的机械能。如果令hw为总流两断面单位重量流体能量损失的平均值,则
![]()
将式(a)、(b)及(c)代入式(4.12),并各项同除以γQ,得
![]()
这就是不可压缩流体恒定总流的伯努利方程,也称能量方程。它与连续性方程一起,是分析流体流动问题的基本方程式。
(4)总流伯努利方程的几何表示
不可压缩实际流体伯努利方程可以用几何表示各项之间的关系。如图4.10所示为一流段,由1—2等直径管段、2—3逐渐扩大锥形管段及3—4的较大等直径管段组成,分别在不同直径连接处接上测压管,将各测压管中液面连接起来得到一条线,称为测压管(水)头线或水力坡线(HydraulicGradeLine)。由此线到管中心的高度表示该断面的压强高度。如果此线位于管中心下方,则表示真空高度。管中心至基准面的高度是位置高度z。在水力坡线上方,沿流程截取表示各断面速度头![]() 的高度,将此高度各点连接起来得到另一条线,称为总(水)头线或能坡线(EnergyGradeLine),能坡线与基准面的距离
的高度,将此高度各点连接起来得到另一条线,称为总(水)头线或能坡线(EnergyGradeLine),能坡线与基准面的距离![]() 表示相应断面上的单位重量流体具有的总机械能。由于有摩阻损失,能坡线总是沿流程下降的。两断面间能坡线的下降值即为摩阻损失,即
表示相应断面上的单位重量流体具有的总机械能。由于有摩阻损失,能坡线总是沿流程下降的。两断面间能坡线的下降值即为摩阻损失,即

至于水力坡线,是沿程上升或下降,要视流动边界的变化及摩阻损失的程度计算确定。沿流程单位长度能坡线的降低值称为能坡线坡度(简称能坡度),以i表示。若能坡线是倾斜直线,则
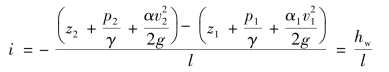
式中,l为两断面间流程长度。若能坡线为曲线,则
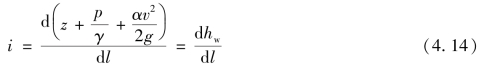
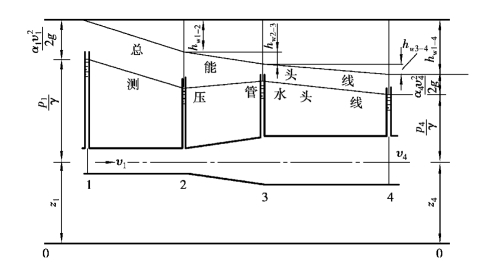
图4.10 能量方程的几何表示
沿流程单位长度的水力坡线的下降(或上升)值称为水力坡度,以ip表示。当水力坡线为直线时,有
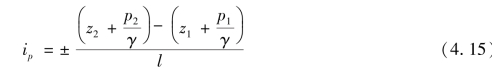
水力坡线为曲线时,有

式中,当水力坡线沿程上升时,取“+”号;相反,取“-”号。在均匀(等直径)流段,能坡线与水力坡线相互平行,i=ip,如图4.10所示。在管流中,能坡线与水力坡线能清晰地表示沿流程单位总机械能及势能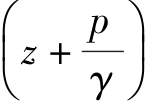 的变化情况。在输油管设计中,常用绘制能坡线或水力坡线的方法来校核压强及确定泵站位置等,因此,是一个很有用的概念。
的变化情况。在输油管设计中,常用绘制能坡线或水力坡线的方法来校核压强及确定泵站位置等,因此,是一个很有用的概念。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






