实际流体流动时，黏滞性将发生作用。而实际流体运动时，除与上一节一样受质量力和压力的作用外，还受因黏滞性而引起的摩擦力的作用。如图4．4所示为以流线为中心轴取一微元柱体隔离体。

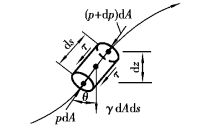
图4．4　在流线上的微柱体

微元柱体的底面积为dA，则作用在柱体两底面的压力为

pdA－（p＋dp）dA＝－dpdA

作用在该柱体侧面的表面力有压力及摩擦力，但压力的方向与运动方向正交，不考虑，而摩擦力的大小为

－τ（2πr）ds

此处τ为切应力。如果质量力只有重力，其沿运动方向的分量为

－ρgdsdA（dz／ds）＝－ρgdAdz

微元柱体的质量是ρdAds，而其加速度的计算，对恒定流来说，可用式（3．17）。因为沿流线，可写作u（du／ds）。因此，按照牛顿第二运动定律，即∑F＝ma，得

这里dA＝πr2，代入并各项除以－ρπr2得

或

式（4．7）对于可压缩或不可压缩实际流体恒定流均适用。

对于不可压缩流体，可以对该式直接积分，积分从某一点1至点2，两点之间的长度是L，则得

或(www.daowen.com)

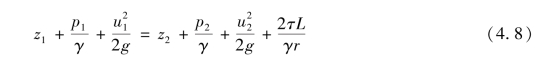
令

则式（4．8）写为

h′w称为摩阻损失（水力学中称为水头损失），它的计算式将在第6章讨论。上式称为伯努利方程，是流体力学中一个重要的关系式。若为理想不可压缩流体，则h′w为零。此时有

在式（4．11）中，第一项z及第二项的物理意义和几何意义在第2章中已介绍过，这里只就第三项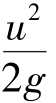的物理意义和几何意义加以说明。是流体在运动情况下产生的，速度为u，质量为m的流体微元具有的动能是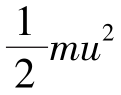，对于单位重量流体来说，应除以mg，即

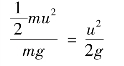
式中，这一项表示单位重量流体所具有的动能。同时，它也具有长度的量纲，所以称为速度水头。上式表明：理想流体中，沿同一条流线上各点单位重量流体所具有的位能、压能和动能三者之间可以互相转化，但三者之和为一常数。它是机械能守恒定律在流体力学的表达式，所以也称为能量方程。从几何意义来说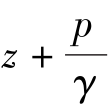，和流体静力学一样，称为测压管（水）能头，而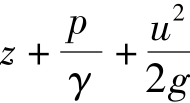称为总能头（或测速管水头）。因此，理想流体沿流线各点的总能头相等。

例4．2 皮托测速管如图4．5所示，明渠水流中，两根皮托管连接在差压计上，差压计中液体的S＝0．82，求uA和uB。

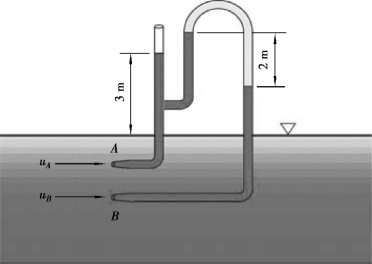
图4．5　皮托测速管

解 因为

所以

由静力学可得

故