除了核物理现象以外,质量守恒定律是自然界中的普遍定律之一,它在流体力学中的具体表现形式就是连续性方程式,它是流体力学中最基本也是最重要的关系式之一。
在过流断面为A1及A2的总流流段(控制体)中任取一流束,其两断面面积和流速分别为dA1、u1及dA2、u2,密度分别为ρ1、ρ2,如图4.1所示。由于微小流束表面是由流线围成的,所以没有流体的穿入或穿出,只有两端dA1和dA2流体的流入和流出。
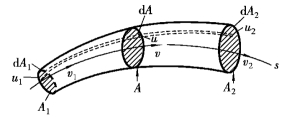
图4.1 连续性方程
现考虑dt时间内,dA1流入的流体质量为ρ1u1dA1;同理,由dA2流出的流体质量为ρ2u2dA2。因此,在dt时间里通过此微小流束的实际流体质量为
dM=ρ1u1dA1-ρ2u2dA2
对于恒定流动,微小流束的形状及各运动参数(如u、p等)都不随时间变化,又因为流体是无空隙的连续介质,所以根据质量守恒定律,在dt时间里微小流束的控制体(dA1及dA2断面所包围的体积)内,流体质量保持不变,即
dM=0
故有
![]()
式(4.1)就是微小流束恒定流时的连续性方程。对于不可压缩流体,ρ=常数,则有
![]()
式(4.2)就是不可压缩流体恒定流束的连续性方程。将式(4.1)和式(4.2)两边沿总流段整个过流断面A1及A2积分,就可得到总流的连续性方程,即
![]()
积分得
![]()
或
![]() (https://www.daowen.com)
(https://www.daowen.com)
式(4.3)表明,对任意流体(可压缩)恒定总流的流动,沿流程的质量流量保持不变,为一常数。式中ρ是断面上的平均密度。
对于不可压缩流体,ρ=常数,则式(4.3)为
或

式(4.4)为不可压缩流体恒定总流的连续性方程。它确定了一元总流在恒定流条件下沿流程保持体积流量不变,为一常数;沿流程各过流断面上的平均流速与其断面积成反比,即断面大流速小,断面小流速大。这是不可压缩流体总流流动的一个基本规律。
注意:式(4.4)是针对控制面侧面无附加流体流入或流出的情况。对于在侧壁有流体的流出,即管道有分支或开岔,如图4.2所示,则根据连续性原理,应有
Q1=Q2+Q3
上式左端表示流入的体积流量,右端表示流出控制体各断面的体积流量之和,因而可得到恒定总流更一般形式的连续性方程为
![]()
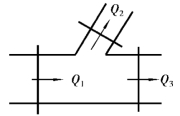
图4.2 管道分支
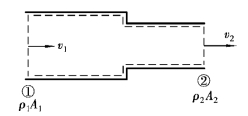
图4.3 串联管流的控制体积
例4.1 一输水管如图4.3所示,断面①的平均流速v1=2m/s,管径为500mm;断面②的管径为300mm,试求体积流量Q及断面②的平均流速v2。
解 由式(4.5)得
![]()
及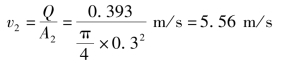
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






