为了简化讨论，取平面运动进行分析。由于流体微团上各点的速度不同，经过dt时段，该流体微团的位置、形状都将发生变化，现在来分析这些是由哪些运动构成的。为此，考虑作平面运动的流体微团在t时刻为ABCD，经过dt后移动到另一个位置成为A′B′C′D′，如图3．16所示，并变形而且转动。由图可知，微团中各点的运动可以分解为：

图3．16　流体的变形运动

（1）平移运动和线变形运动

平移运动和线变形运动，即由A点平移至A′点所构成的运动，并设想在运动过程中，形状不变。其移动距离为uxdt、uydt，移动方向由A点t时刻的速度方向所确定。

流体微团上各点由于位置不同会引起速度的变化，这将使得流体微团在dt时段内产生沿坐标轴方向的线变形，即各边伸长或缩短。如图3．16所示，AB和AD边经过dt时段后变为A′B′和A′D′所形成的线变形为

用ε表示单位时间单位长度的线变形（称为线变率），则有流体微团沿x方向的线变率为

同理，有

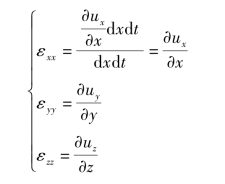
上式即为式（3．29）矩阵中主对角线的三个元素。流体微团的体积膨胀率ε为x、y、z三个方向上线变率之和，即

（2）角变形运动和旋转运动

角变形指流体微团中某一平面角在变形前后的变化量。由图3．16中的几何关系可知，变形角度dβ1为

同理，有

习惯上将单位时间的角变形之半定义为角变率。因角变形发生在xOy平面上，故用εxy表示，即

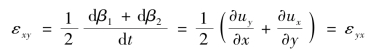
推广到三维，则有流体微团的角变率为

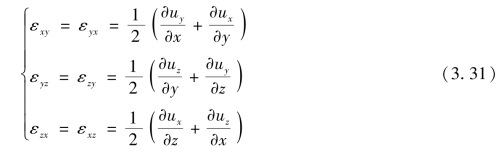(www.daowen.com)

角变形的不同还会引起旋转。旋转指的是流体微团运动前后角平分线的位置是否有变化。如在图3．16中，运动前角平分线为AC，运动后角平分线为A′C′，它们之间的夹角为dθz，即为旋转角，反映变形前后主对角线的变形，其下标z表示xOy面上ABCD绕z轴旋转。由图可见，dθz与dβ1、dβ2有关，但在旋转情况下，应考虑转角的正负性（逆时针为正，顺时针为负）。单位时间的旋转角变形（角变率）称为旋转角速度，用ω表示，即

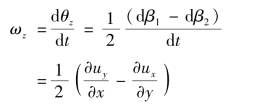
同理可得ωx、ωy，所以，流体微团的旋转角速度分量为

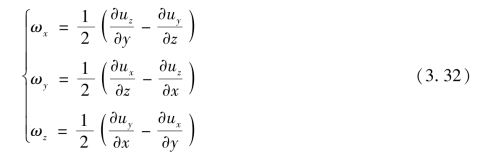
或

根据流体微团运动分析所得出的表达式，可对式（3．28）M点的速度分量进一步变换。因为

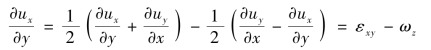
同理

将这两个关系代入式（3．28）得第一式，简化后可得

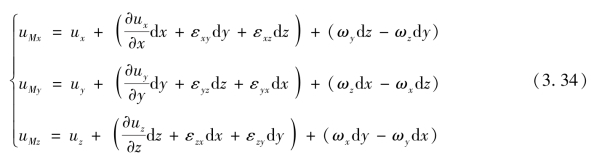
式（3．34）即为流体微团的速度分解定理。式中可分为三个部分：第一部分为平移速度；第二部分为变形速度（包括线变形和角变形）；第三部分为旋转速度。

例3．3 设有平面流场，ux＝x2y＋y2，uy＝x2－y2x，求此流场在点（1，2）处的线变率，角变率和旋转角速度。

解 因是平面流场，uz＝0，线变率：

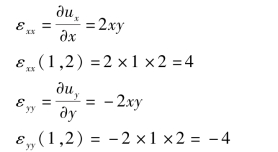
角变率：

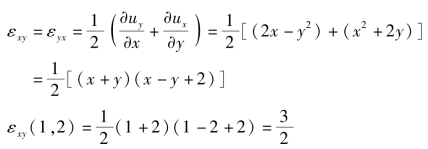
旋转角速度：