在第2章中，导出以流体平衡微分方程式（2．3）或式（2．4），是针对一个系统的。在流体运动学中，需要研究系统的力学规律，但由于流体流动的复杂性，对于研究对象的取法有很大的影响。实际上在前面的分析问题中提到了取隔离体的概念，它本质上指的就是控制体。

所谓系统，指的是一团流体质点的集合。它包含有确定的质量，系统的外界形成一个封闭的表面，称为边界。一个系统可以随着运动的变化而改变它的形状和空间位置，但它包含的物质质量不随运动改变。

所谓控制体，指的是流场中某一个确定的空间区域，它的边界称为控制面。控制体的质量可以随时间变化，但它的形状及空间位置不变。如图3．13所示，系统状态Ⅰ，其边界用虚线所示，体积为V0，而此时的控制体和系统重合，控制面用实线表示，体积为V，且有V＝V0。在t＋dt瞬时，系统的位置和形状改变，体积也变成V′，但系统的质量不变；而此时的控制体，其位置和形状未变，体积未变，仍为V0，但质量已有改变，如图3．14所示。

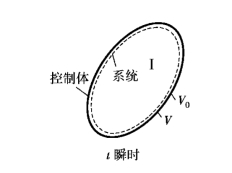
图3．13　t瞬时的系统与控制体(www.daowen.com)

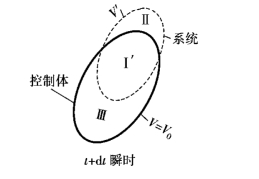
图3．14　t＋dt瞬时的系统与控制体

流体力学所研究的是系统的物理量，但这些量的变化又与所选定的控制体有关。控制体积的大小和形状完全是任意的，有些部分常取其与固体边界相重合，有些边界为了分析简便取与流速方向垂直。而系统可以按照自身运动规律穿越控制体表面流入流出该控制体。

由于流体有极大的流动性，使得识别一个特定的系统成为一个十分复杂而艰难的问题。而利用控制体的方法，既可以克服对系统辨别上的困难，又能使对流体分析大为简化。因此，在本章的若干节里，将分别把基本物理定律从系统方法转换为控制体方法，导出这些定律在流体力学中的表达式。