（1）迹线

流场中某一流体质点运动的轨迹称为迹线。它表示同一流体质点在不同时刻的运动方向。拉格朗日法是研究流体质点的运动情况的，用拉格朗日法可直接得到迹线方程。在拉格朗日法中，式（3．2）就是质点迹线的参数方程。

（2）流线

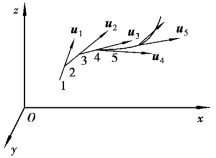
图3．7　流线

流线是某一瞬时在流场中绘出的一条曲线，在该曲线上各点的速度矢量相切于这条曲线。设想在流场u＝u（x，y，z，t）中（见图3．7），任取一点1绘出t瞬时点1上的速度矢量u1，在u1矢量线上取与点1相距极近的点2，绘出同一瞬时点2的速度矢量u2，再在u2的矢量线上取与点2相距极近的点3，绘出同一瞬时点3的速度矢量u3，以此类推，就可得到1、2、3、4出发的一条流线。流线可以形象地描述出流场内的流动状态。假如在流场各空间点都绘出同一瞬时的流线，那么这些流线的综合就可描绘出整个空间在该瞬时的流动图景。例如，将细的铝粉末撒在流动的水流表面上，进行曝光时间极短的快速摄影，则在照片上可以得到表示比例于流速u的大小和方向的小线段。若所撒的颗粒适当加密，将那些小线连接起来就可以得到表示速度方向的流线谱，此流线谱就展示了该瞬时流场中的流动图景。

流线具有下列两个特性：

①在恒定流时，因为流速场不随时间而变化，则流线的形状也不随时间变化。同时，经过某一共同点的流线和迹线相互重合，因此，流体质点沿着流线运动而决不离开流线。非恒定流时只有瞬时流线，不同瞬时，一般说来有不同的流线，因此，流线与迹线不相重合。

②根据流线定义，通过某一空间点在给定瞬时只能有一条流线，一般情况下，流线不能相交和分支，否则在同一空间点上流体质点将同时有几个不同的流动方向。只有流速场中速度为零或无穷大的那些点，流线可以相交，这是因为在这些点上会出现在同一点上存在不同的流场方向的问题。

（3）流线微分方程式

根据流线的定义可以导出流线的微分方程式。在流场中取一点M，在某瞬时t通过点M的流线s如图3．8所示。

在流线上从点M取一微段ds，可以将它近似成直线，它在坐标轴的投影为dx、dy、dz，因为流线上每一点的速度向量均与流线相切，过点M的速度向量u可以看成与ds重合，u在坐标轴方向的分量为ux、uy、uz，则方向余弦为

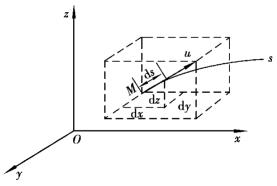
图3．8　流线微分方程式

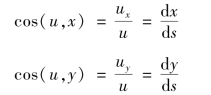
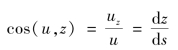
由此可得

这就是流线的微分方程式，式中ux、uy、uz都是（x，y，z）和t的函数。不同瞬时有不同的流线，时间t是流线方程的参变数。

用矢量表示的流线方程为(www.daowen.com)

式中，r为空间某点的向径，dr为流线的微元长，如图3．9所示。

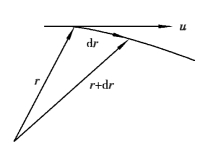
图3．9　速度及向径矢量

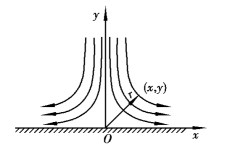
图3．10　双曲线形流线

例3．2 有一ux＝cx，uy＝－cy，uz＝0的速度场，其中c为常数，且y≥0，试求流场中质点的加速度及流线方程。

解 从uz＝0及y≥0，可见流体运动只限于xOy坐标系的上半平面。

①质点的速度

因为

则质点的加速度

故

②流线方程

由流线微分方程式（3．19），得

消去c，积分得

lnx＝－lny＋lnc

即 xy＝c

流线如图3．10所示的一簇等角双曲线，质点离原点越近，即r越小，其速度和加速度均越小，在r＝0处速度与加速度均为零。流体力学中称速度为零的点为驻点或滞止点，图中O点即是。相反，在r→∞的无穷远处，u及a均趋于无穷大，流体力学上称速度趋近无穷大的点为奇点，驻点和奇点是流场中的极端情况。一般流场中不一定都存在驻点或奇点。