欧拉法只着眼于流场各固定点，研究各瞬时这些点的流动情况，而无论这些运动情况是由那些质点表现出来的，也无论这些质点的来龙去脉，而将流体的速度u、压强p、密度ρ等运动参数作为空间点坐标（x，y，z）和时间t的函数而论述的一种方法。以u为例：

或

在式（3．8）中，如令（x，y，z）为常数，t为变数，可以得不同瞬时通过空间相应固定点的流体流速的变化情况；如令t为常数，（x，y，z）为变数，则可得同一瞬时在流场内通过不同空间点的流体流速的分布情况，即此时瞬时的速度场。如令（x，y，z）及t均为变数，则研究的对象将是任意时刻t通过空间任意点（x，y，z）的流体质点的运动情况。

在欧拉法中，当时刻t时，假设流体质点由空间位置和时间所确定的物理量为θ（x，y，z，t），则该质点的物理量θ对时间的变化率为，根据多元偏导数的概念可得

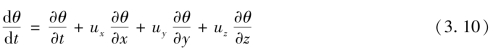
称dθ／dt为流体力学的质点导数，式（3．10）也可写为

式中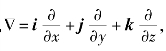，称为哈密顿算子（Hamiltonianoperator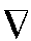，“”读作“del”或“nabla”）。作为例子，假设质点的位置向量为r（x，y，z，t），按照速度物理意义，表示的应该是速度u，而实际上，若取r的分量x，y，z作为式（3．10）的θ（注意：在欧拉法中，（x，y，z）和t是独立变数），则

同理

(www.daowen.com)

又若取速度u作为θ，则可得到加速度的表达式为

写成分量形式，即

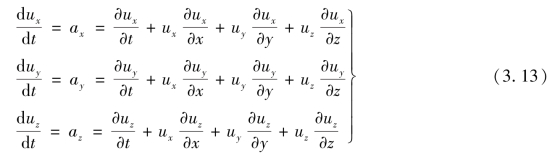
由式（3．12）或式（3．13）可知，用欧拉法求得的流体质点的加速度由两部分组成：第一部分为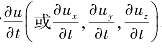称为当地加速度或时变加速度，它表示在某一固定空间点上因时间的变化而引起的速度变化率。第二部分为（u·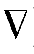）u（或式（3．13）中的后三项之和），称为迁移加速度或位变加速度，它表示流体质点在dt时间内从该固定点作微小位移（位变）过程中，由于流场随空间位置变化的非均匀性，引起质点速度的变化率。对于均匀流场，这部分的加速度应等于零。当地加速度及迁移加速度的物理意义可以图3．6所示的简例说明。装在水箱的水经过水箱底的一段等径管路AB及变径喷嘴BC向外流出。设管轴上有1、2、3三个点，在点1和点2位于等径段上，点3位于变径管上。若箱中水位保持恒定，则质点由点1流向点2时既没有当地加速度也没有迁移加速度；质点从点2流向点3时，虽没有当地加速度，但却有迁移加速度。如果箱中水位不断下降，质点从点1流向点2时，虽然没有迁移加速度，但却有当地加速度；而质点从点2流向点3时，既有当地加速度，又有迁移加速度。

例3．1 在图3．6中，若点2的速度u2＝4m／s，点3的速度u3＝8m／s，点2至点3的距离l＝0．4m，试求点3的迁移加速度。

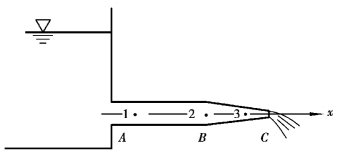
图3．6　当地加速度和迁移加速度

解 因为沿管轴线上流动为一元流，则由点2到点3的速度梯度为

故点3的迁移加速度为