这是一种追踪流体质点历程的方法，所以也称为跟踪追迹法。它实际上是承袭一般力学里求质点的轨迹一样，研究流体中每一质点随时间在空间位置的改变，同时观察和分析各质点在运动历程中各运动参数的变化，综合足够多质点的运动情况后，便得到整个流体运动规律。

由于这一方法是以流体质点作为研究对象，因此需识别不同的质点。设在某一时刻t0，质点的位置由它的起始坐标a、b、c所确定。显然，该质点在任何时刻t的位置将是该质点的起始坐标a、b、c及时向t的连续函数。如以r表示质点在时刻t的向径，则

r在x、y、z轴上的投影，分别为

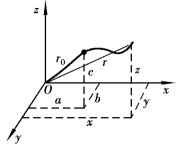
这里用来识别不同的流体质点的起始坐标a、b、c都应当作是自变量，它们和时间t一起称为拉格朗日变量。拉格朗日变量是各自独立的，质点的初始坐标（a、b、c）与时间t无关，这样r或x、y、z只是时间t的函数。在这种情况下，式（3．1）或式（3．2）所表达的是流体质点运动的迹线（或轨迹）如图3．5所示。

如果要求得某一质点在任一瞬时t时的速度向量u，只要将式（3．1）对时间取偏导数即可，即

(www.daowen.com)

图3．5　拉格朗日法

其在x、y、z轴向的分量分别为

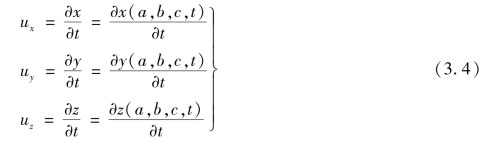
在求得上述的偏导数以后，如令a、b、c为常数，t为变数，则可得出某一质点在不同时间中的速度变化情况；反之，如果令t为常数，a、b、c为变数，则可得某一时刻流体内部各质点的流速分布情况。

流体质点的其他流动参数如压强p、密度ρ、温度T等也可以用类似的方法予以表示，即

拉格朗日法是直接研究流体质点的运动，似乎是一个很简单很具体的方法，但实际上由于流体质点不像固体质点那样受到较大的约束，追踪质点是一个很复杂的问题，在数学处理上非常麻烦和困难，因此，除了少数特殊问题（如紊动的扩散作用）外，极少使用，实用上，并无必要知道每一个流体质点的详细历史，只要能描绘出每一时刻流体运动参数在流场中每一固定点上的数值及其变化规律，而不必关注那些质点究竟在什么地方。例如，欲确定作用在流场内一个静止物体上的力，就要求知道物体上各点的压强和切应力，而无须知道这些点上的压强和切应力是由哪些质点作用的。提供这一简便方法的就是流体力学中广泛采用的第二种方法——欧拉法。