在研究流体运动时，要涉及液体和气体，气体比液体可压缩得多；但是，在任何一个具体的流动过程中，压缩是否发生到显著的地步，对于显著的压缩，必有可观的压强变化。如果气流的速度不大，气体所展布的高度不高，流动有效断面又不太大，则压强的变化就远比平均压强小，于是体积的变化就很小，为了简化计算，体积的变化一般就可以完全忽略不计。在这种情形下，气体的流动就与不可压缩的液体的流动毫无区别。假设1%的体积变化认为可以忽略，就可以将关于不可压缩液体流动的公式应用到常温下的空气、天然气等的流动中去。例如，只要它的流动速度不超过约50m／s，而高度不超过100m时就可以应用，何况在速度为150m／s时，体积的改变只约为10%。但当流速变得和声速（约340m／s）同数量级的时候，体积的变化就很可观，而使流动状况（流场特征）起显著的变化。当流速超过声速的时候，流动的特征甚至完全不同于平常液体的一般情况。

在本书中，除了第8章、第11章讨论体积变化不可忽略的一元流动基本理论外，本章及以后其余章节，均讨论体积变化忽略不计的情形。

与静止或相对静止情况不同，流体在流动的时候，流体的黏滞性将发生作用。因此，在流动中除了受质量力、压力外，还受到流体抵抗变形的黏性阻力（内摩擦力）的作用。由于黏滞性的作用，在流动流体中，任一点上的压强（称为动压强）不仅与该点的所在空间位置有关，也与方向有关，这就与静压强有所区别。但是，经理论推导证明（见第10章），流动流体中任一点在三个正交方向的压强的平均值为一常数，即

式中p是一常数，它不随这三个正交方向的选取而变化。这个平均值就作为点的压强值。在本章及以后的章节中，流动流体的动压强和流体的静压强，一般在概念和命名上不予区别，一律称为压强。

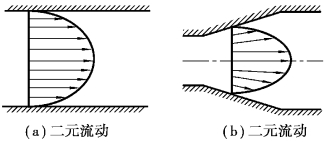
由于流体具有黏滞性，流体与固体壁面有黏附作用，因此，流体在固体壁面上没有滑移现象，在垂直于流动方向上常有速度梯度，如图3．1所示。因此，实际流体流动时至少是二元的，一般情况下多为三元流。例如，将飞机模型放在风洞中，使风洞中的风呈均匀流动，这时飞机周围的流动是三元的复杂流动，如图3．2所示。但是，三元流的分析一般是非常困难的，所以多用二元模型来代替，作为二元流动进行分析。如上例的飞机，可用像图3．3所示的那样翼型周围的流动来分析，就可作为二元流动来处理。在许多实际工程问题中，流体的运动参数（速度、压强、密度等）在正交于主流方向上的变化与沿主流方向的变化比较起来很小，因而可以忽略不计，这时可以将它简化为一元流。例如，管道中的流体主要沿管轴方向流动，河渠中的水流主要沿河渠主流轴线方向流动。虽然严格来讲是属于二元流动，但是它们的流速常常用断面平均流速（见图3．4）来描述，认为断面上各点的速度是均匀分布，其运动参数只沿主流方向变化。这样，就可以沿流动的主流方向选取坐标（一般情况下是曲线坐标），将整个流股（总流）作为研究对象，分析运动参数沿主流方向的变化规律及相互关系，从而可使问题大为简化，避免复杂的数学分析。这样的处理，从实际应用的目的往往是足够正确的。

(www.daowen.com)

图3．1　二元流

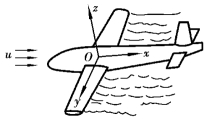
图3．2　三元流动

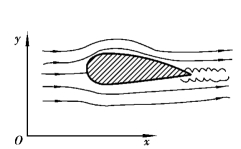
图3．3　二元流动（翼型）

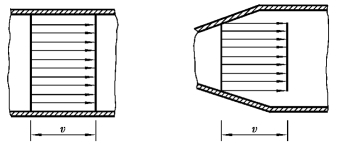
图3．4　一元流动