在式（2．41）中，将sinαdA＝dAz，p＝p0－pa＋γh代入，得

从图2．28可知，γhdAz为微小曲面dA与其在自由液面的投影面dAz之间的液柱重量。由此看出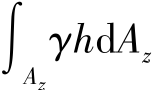，z表示整个曲面AB与其在自由液面（有时是自由液面的延长面）上的投影面Az之间所构成空间的液体重量，即图中ABCD空间的液体重量。因此，上式的积分结果可写为

式中，Vp称为压力体。力γVp的作用线通过压力体Vp的重心，而（p0－pa）Az的作用线通过Az的形心。

压力体是一个重要概念，它是由曲面本身及其在自由液面（或自由液面的延长面）的投影面与从曲面的周边引至自由液面的铅垂侧面所组成的体积。换句话说，压力体的底面为所研究的曲面本身，它的顶面是该曲面在自由液面（或自由液面的延长面）的投影面，其侧面为沿该曲面边缘引向自由液面的铅垂面所构成。计算压力体的“液重”这一部分压力时，要特别注意其方向。它可能有两种情况：一是像上述所分析的情况，此时压力体中都充满了液体，如图2．29（a）所示的阴影部分，VP＝体积ABCD，这部分的“液重”对曲面的压力是向下的，称为实压力体。相反，假使液体位于曲面的右侧，同是曲面AB，按照压力体的定义，其压力体的体积VP＝体积A′B′C′D′，如图2．29（b）所示的斜阴影部分。它与左边的压力体ABCD相等，但内部并无液体，这部分的“液重”对曲面的压力是向上的，称为虚压力体。由此得出结论：当压力体与液体都位于曲面的同一侧时，压力体的“液重”对曲面的压力是向下的；相反，当压力体与液体不在曲面的同一侧时，其对曲面的压力是向上的。对于较复杂的曲面，例如，卧式油罐（图2．30）曲面abc部分的压力体，ab段的压力体为体积abcd，液体与压力体都位于曲面ab的同侧，对曲面ab的压力向下，为实压力体（图2．30（a））；bc段的压力体为bcd（图3．30（b）），压力体与液体不在曲面的同一侧，对曲面bc的压力是向上的，为虚压力体。整个曲面abc的压力体应为这两部分压力体的代数和，由于体积bcd部分为两段曲面所共有，其压力大小相等而方向相反，因而互相抵消，所以曲面abc的压力体最后为如图3．30（c）所示的阴影部分，为实压力体，压力方向向下。

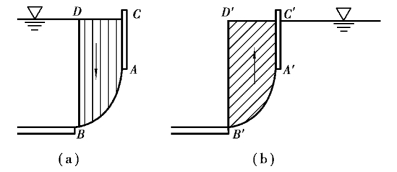
图2．29　压力体

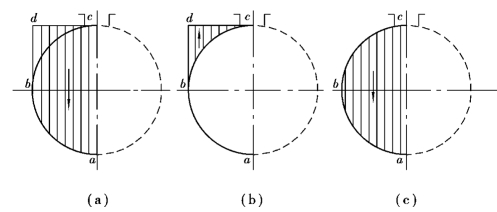
图2．30　abc曲面的压力体

例2．10 如图2．31所示为一立式圆柱形储油罐，内装密度ρ＝730kg／m3的汽油。已知油罐直径D＝15．25m，装油高度H＝9．6m，油罐内液面上的表压强为220mm水柱。求罐身半个壁面的流体总压力和罐顶铅垂向上的总压力各为若干。

解 ①罐身的半个罐壁的流体总压力

因为罐身垂直安装，罐身只有水平总压力，由式（2．42）得

Fx＝（p0－pa）Ax＋γhCAx

式中：

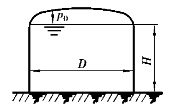
图2．31　立式柱形储油罐

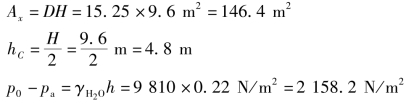
代入式（2．42）中得

②罐顶的总压力

因为罐顶上压力体vp等于零，由式（2．43）得

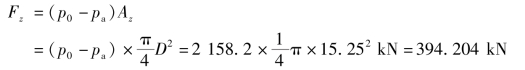
例2．11 有一敷设于地上的管路如图2．32所示，管内表压强为p，试确定当管材抗拉强度为［σ］，管壁厚度δ与压强p及D之间的关系式（按薄壁管计算，只考虑周向（环向）拉应力，纵向拉应力忽略）。

解 为了分析方便，截取单位长度管段并沿直径切开，取其一半分析其受力的作用。

因为管内压强p通常很大，忽略液体重量影响，认为压强均匀分布。图示z方向的压力互相抵消，只有x方向的分压力Fx，它与拉力T平衡，因Ax＝d×1，故(www.daowen.com)

T＝Fx＝pAx＝pd

根据强度理论

T≤2δ×1×［σ］

则

设计管道时，如果不考虑其他载荷，可用该公式确定壁厚。

图2．32　管路

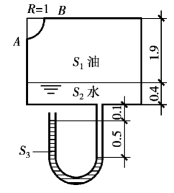
图2．33　压力储油箱

例2．12 如图2．33所示的压力储油箱垂直纸面的宽度b＝2m，油品相对密度S1＝0．8，油层下有积水，箱底装有一U形测压计，S3＝13．6，相关尺寸如图所示，试求作用在圆柱面AB上的总压力的大小。

解 先求出B点的压强

pB＋γ1×1．9＋γ2（0．4＋0．1＋0．5）＝γ3×0．5

则pB＝9810×（0．5×13．6－0．8×1．9－1×1）Pa＝41986．8Pa

水平方向的压力为

Fx＝PBAx＋γhCAx

式中，Ax＝1×2m2＝2m2

hC＝0．5m

则 Fx＝（41986．8×2＋0．8×9810×0．5×2）N＝91．8kN

垂直方向的压力

Fz＝pBAz＋γV压

其中：Az＝1×2m2＝2m2

则 Fz＝（41986．8×2＋0．8×9810×1．57）N＝96．3kN

总压力为