工业中的各种流体容器，尤其大型容器，其壁面几乎都制成曲面的形状。例如，立式和卧式储油罐的罐身、罐顶，球形罐的整个罐壁都是曲面的。在水利工程方面，如弧形闸门、拱坝的表面等也是曲面的。因此，学会计算作用在曲面上的流体总压力，在工程中有着特别重要的意义。

由于曲面上各点的法线方向不同，既不平行也不一定交于一点，因此，作用在曲面各微元面积上微元压力的大小和方向各不相同，为空间力系，不能用前面求平面总压力的方法直接积分求解。但是，可通过计算它的水平分量和铅直分量的方法来确定。方法是将作用在曲面各微元面积上的压力dF分解为Fx、Fy、Fz，则得到三组平行力系，分别进行积分求其代数和，便得到总压力的三个分量Fx、Fy及Fz，由此可求得其合力F，即

为了便于分析，下面以二元曲面（即具有平行母线的柱面）为例，说明总压力的计算方法，所得结论可以推广到任意曲面。

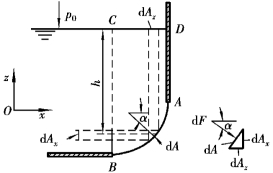
图2．28所示为盛装液体的容器。其壁面AB部分为二元曲面，其母线平行于Oy轴，即垂直于纸面。

(www.daowen.com)

图2．28　曲面上的总压力计算

设液体自由液面的绝对压强为p0，不一定等于大气压。在曲面上任取一微元面积dA，其形心点深度为h，则作用在dA面上的压力dF＝pdA，其在x、z轴上的分量为

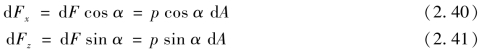
式中，α为dF与水平平面的夹角。根据几何关系，cosαdA是dA在x向的法平面（即垂直于x轴的平面）上的投影面积，即cosαdA＝dAx，同理，sinαdA＝dAz。

另外，式中压强p应为相对压强，即p＝p0－pa＋γh。将上述关系代入式（2．40）及式（2．41），并积分便得到总压力的水平分量和铅直分量。