总压力作用线与作用面的交点称为作用点，也称为压力中心，以M表示。

分析式（2．35）可知，总压力F由两部分组成：一是（p0－pa）A，二是γhCA。前者因相对压强（p0－pa）在整个面积A上均匀分布，所以（p0－pa）A这一部分压力的作用点位于形心上；而后者因为是液体重力引起的压强对平面作用的结果，此压强随深度而增加，其压力的作用点必然在形心C的下边。设点D表示该压力的作用点，根据力学上合力对某轴的力矩等于各分力对同轴的力矩的代数和原理，可求得总压力的作用点M的位置。

按照这个原理，总压力F对Ox轴的力矩，应该等于微小压力dF对Ox轴的力矩之和，即

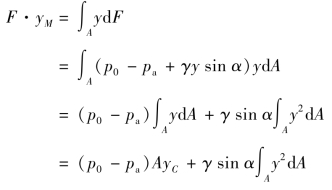
式中，∫Ay2dA是面积A对Ox轴的惯性矩，用符号Ix表示，即

F·yM＝（p0－pa）AyC＋Ixγsinα

根据惯性矩平移定理，Ix＝IC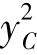＋A，则上式变为

F·yM＝（p0－pa）AyC＋（IC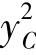＋A）γsinα

得压力中心计算公式为

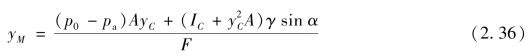
或

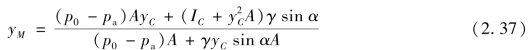
式中，IC是平面A对通过形心C并且平行于Ox轴之惯性矩。

如果p0＝pa，则式（2．37）变为

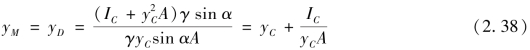
即此时作用点M与D点重合。

因为恒为正值，所以yM＞yC，即总压力作用点M永远在平面形心C的下边。至于作用点M的x坐标，可用类似的方法求得。不过在工程实践中，平面图形常常是对称的，所以通常只需求得作用点的y坐标即可。常见平面图形的IC、yC及A值见表2．1。

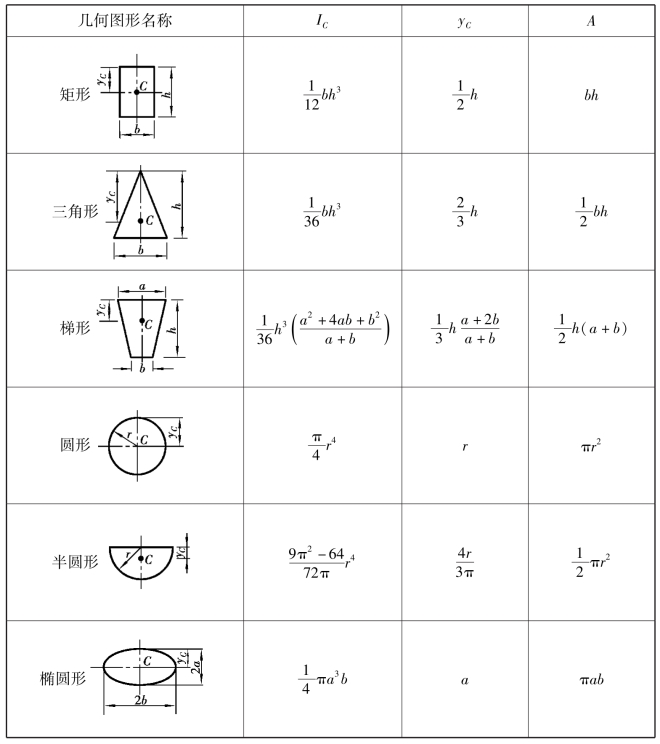
表2．1　几种平面图形对于通过形心轴的惯性矩IC、形心坐标yC及面积A之值

例2．8 如图2．26所示，上部是矩形断面而下部是三角形断面的水道，在入口处设置同样形状的闸门，求作用在闸门上的液体（水）总压力及作用点（压力中心）。

解 将闸门分成矩形和三角形断面两部分，分别求出作用在它们上液体总压力及作用点，然后算出总的结果。

①矩形断面的总压力F1及作用点hD1因为p0＝pa，所以

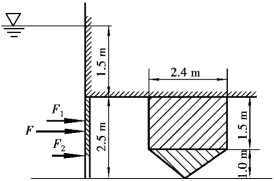
图2．26　闸门

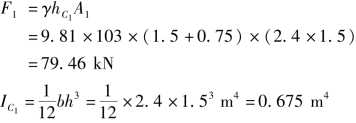(www.daowen.com)

由式（2．38）得

②三角形断面上的F2及hD2

三角形的特征量由表2．1查得。这里b＝2．4m，h＝1．0m，图形形心位置距上边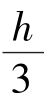，得

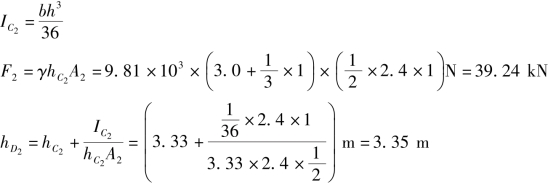
③总压力F及其作用点hM

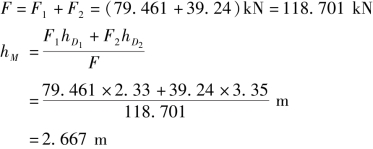
例2．9 图2．27为储油罐内部保险阀。已知阀板为椭圆形，长轴2b＝120mm，短轴2a＝112mm，重力19．61N，H＝5m，γ＝7651N／m3，求开启阀门时所需拉力T。

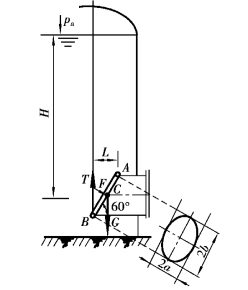
图2．27　油罐内部保险阀

解 由表2．1查得椭圆形特征量

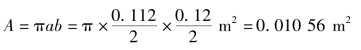
惯性矩IC是对长轴的公式，本题应为

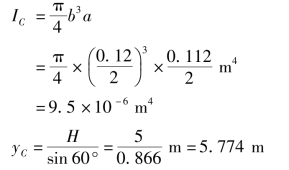
①总压力大小F

F＝γhCA＝7651×5×0．01056N＝404N

②作用点yD

由式（2．38）得

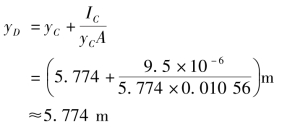
计算结果表明，当受压面的形心深度较大，受压面又较小时，近似地认为作用点位于形心上。

③拉力T

将各力对A点取矩，得

式中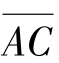， ＝b＝0．06m，L＝2bcos60°＝2×0．06×cos60°m＝0．06m，代入上式，得