如图2．10所示，如果液体中任一点1上流体微元的质量为m，它相对于某一水平基准面的高度为z1，具有的位置势能是mgz1；另外，点1上的压强为p1。如果用一根下部与点1连通、上部密闭并抽成完全真空的玻璃管（测压管）连接起来，在p1的作用下，液体上升到h1的高度，玻璃管内液面上的压强为零（完全真空），根据式（2．13）得

由此可见，液体上升的高度h1是压强p1做功的结果。根据物理学，若位于点1上的液体微元的体积为δV，则该流体微元具有的压能为

图2．10　流体静压强基本关系式的物理意义及几何意义

点1上流体微元具有的总能量应为其位能和压能之和，即

(www.daowen.com)

除以mg，得

由此可见，z1表示该点单位重量液体相对某水平基准面具有的位能，即比位能；表示该点单位重量液体具有的压强能（即比压能）。因为位能和压强能均属势能，因而表示点1上单位重量液体具有的势能（简称单位势能）。因此，流体静压强基本方程式（2．12）的物理意义是静止液体内各点的单位势能相等。例如，在图2．10中的点2，接上与点1一样上端密闭并抽成完全真空的玻璃管，则液体上升高度。应该有

图2．11　开口测压管与闭口测压管比较

从几何角度，流体力学中习惯将高度称为头。式（2．12）中，z称为位置头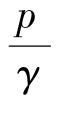，称为压强（水）头，z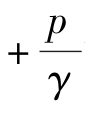称为测压管（水）头。因而流体静压强基本方程式的几何意义表示静止液体内各点的测压管（水）头相等。测压管抽成完全真空是不可能的，实际的测压管顶端往往是开口连通大气，如图2．11所示。这样，开口测压管中液体上升的高度要比抽成完全真空的闭口测压管低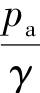这一段的液柱高度。因而开口测压管所示的高度为该点相对压强所对应的压强（水）头。