对于连续、均质的不可压缩流体，其密度为常数，式（2．11）可写为

在流体连续区域内积分，可得

这就是连续、均质不可压缩流体中静压强基本公式，积分常数C可由边界条件确定。如图2．6所示，若已知液面上的铅直坐标为z0，压强为p0，则，则式（2．12）写为

移项得

p＝p0＋γ（z0－z）

由图中关系得z0－z＝h，所以上式可表达为十分直观的压强分布规律公式，即

式中，h是液体中任意点在自由液面下的深度，简称深度。由式（2．13）看出：

①在静止液体中，任一点的压强p由两部分组成：一部分为表面压强p0；另一部分是从该点到表面（或自由表面）单位面积上的液柱重γh。

②表面压强p0等值地传递到液体内各点。

③位于同一深度的各点具有相同的压强值。也就是说，质量力只有重力作用下的平衡液体内等压面为水平平面，证明了等压面与质量力方向垂直。因此，在静止的液体中，只要作一水平平面，就是等压面。但要注意这个结论必须具备两个前提：一是质量力只有重力作用的静止液体；二是液体区域必须是由同一种均质液体连通起来。如果是连通但非均质的液体，或者均质的液体之间隔有气体或另一种液体，则其中同一水平平面就不再是等压面。如图2．7所示，Ⅰ⁃Ⅰ是一水平平面，但容器中点1与细管中点1′不是同一种液体，点1上的压强不等于点1′上的压强。相对于容器和细管中液体而言，Ⅰ⁃Ⅰ不是等压面。而水平平面Ⅱ⁃Ⅱ及Ⅲ⁃Ⅲ则为等压面，因为都通过同一种液体中。此时，p2＝p′2，p3＝p′3。

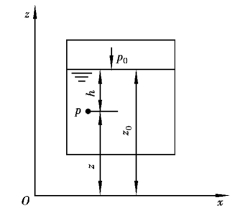
图2．6　重力场中静止液体内的压强分布

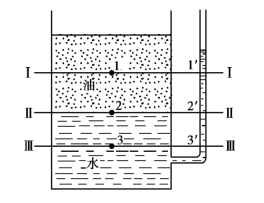
图2．7　等压面概念

等压面概念十分重要，在应用基本方程式（2．13）时，常借助等压面概念来解决工程计算问题，尤其在液柱式测压仪器计算中，经常要用到，必须很好地掌握其运用方法。(www.daowen.com)

例2．1 已知油罐中液面上的压强p0＝102000N／m2，油的密度ρ＝680kg／m3，g＝9．81m／s2，试求油面下深度为7m处的压强是多少？

解 根据式（2．13）得

p＝p0＋ρgh＝（102000＋680×9．81×7）N／m2＝148．7kN／m2

例2．2 如图2．8所示，容器内盛装相对密度S＝0．9的油品，A点上的大气压强为标准大气压（101325N／m2），C与A点位于同一水平面上，h1＝6m，h2＝9m，求B、C及D点上的压强。

解 ①B点的压强

因为B点相对于A点的深度为h2，由式（2．13）得

pB＝pA＋ρgh2

＝（101325＋900×9．81×9）N／m2

＝180786N／m2

＝181kN／m2

②C点的压强

因为C点与A点位于同一水平面上（等压面），故pC＝pA＝101325N／m2。

③D点的压强

因为pC＝pD＋ρgh1，由此得

pD＝pA－ρgh1＝（101325－900×9．81×6）N／m2＝48351N／m2

≈48．4kN／m2

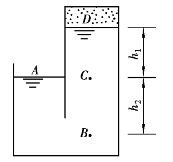
图2．8　例2．2图